Bước tới nội dung

Vật thể bất khả thi

Bách khoa toàn thư mở Wikipedia

Một Vật thể bất khả thi, Hình bất khả thi, hay Hình bất khả quyết (tên tiếng Anh: Impossible Object, impossible figure, undecidable figure) là một loại ảo ảnh quang học, tức là nó là một vật thể 2 chiều như tồn tại trên giấy nhưng khi quan sát thì các loại ảo ảnh thị giác lại gây cho ta cảm giác như đó là một đối tượng 3 chiều.[1]

Tam giác Penrose, ví dụ điển hình cho vật thể bất khả thi

Ở đây ta có thể hiểu đơn giản như với tam giác Penrose, lúc đầu khi ta nhìn thấy nó là 3 cạnh liền nhau tạo bởi các chùm đường thẳng vuông góc với nhau từng đôi một có vẻ không mâu thuẫn nhưng khi nhìn tổng thể thì rõ ràng các đôi một đường thẳng vuông góc không cùng nằm trên một mặt phẳng.

Trong đa số trường hợp, tính không thể có thể thấy ngay sau vài giây, chẳng hạn như tam giác Penrose hay "con voi nhảy múa". Tuy nhiên, ấn tượng ban đầu của vật thể 3D vẫn còn ngay cả sau khi nó đã bị mâu thuẫn. Ngoài ra còn có những ví dụ tinh tế hơn về các vật thể không thể xảy ra nếu sự không thể xảy ra không rõ ràng một cách tự nhiên và cần phải có ý thức kiểm tra hình học của đối tượng ngụ ý để xác định rằng nó là không thể.

Bản chất không ổn định của các vật thể không thể xảy ra do mong muốn tự nhiên của chúng ta để giải thích các bản vẽ 2D như các đối tượng ba chiều. Đây là lý do tại sao một bản vẽ của một khối Necker sẽ được xem như là một khối lập phương, chứ không phải là "hai ô vuông nối với các đường chéo, một hình vuông bao quanh bởi các hình phẳng phẳng bất thường hoặc bất kỳ hình phẳng nào khác." Với một đối tượng không thể, nhìn vào các phần khác nhau của vật thể làm cho ta tính lại được bản chất 3D của vật thể, điều này làm cho trí tuệ bối rối.  Các đối tượng không thể được quan tâm đến các nhà tâm lý học, toán học và nghệ sĩ mà không rơi vào hoàn toàn bất kỳ kỷ luật nào.

Các ví dụ nổi bật

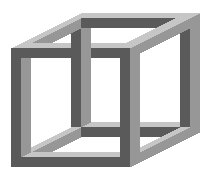
[sửa | sửa mã nguồn]

1. Khối lập phương không thể- Các khối lập phương không thể được phát minh bởi MC Escher cho Belvedere , một tờ in đá, trong đó một cậu bé ngồi dưới chân của tòa nhà chứa một khối không thể. Ở hình dưới, để ý rằng tất cả các cạnh của hình lập phương đều thấy được và không có cạnh nào bị khuất. [2]

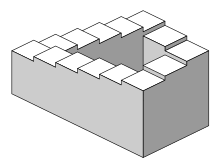
2. Cầu thang Penrose-Penrose được tạo ra lần đầu tiên bởi họa sĩ người Thụy Điển Oscar Reutersvärd năm 1934. Nhà toán học Roger Penrose tự phát minh ra và phổ biến nó vào những năm 1950, mô tả nó như là "không thể thực hiện được theo hình thức tinh khiết nhất của nó [3], bạn có thể xem một video về chiếc cầu thang này: https://www.youtube.com/watch?v=GquGqB2NPLM Để ý kỹ trong hình dưới, bạn sẽ thấy nếu lấy 4 điểm tương ứng của 4 cạnh cầu thang thì chúng đều có cùng một độ cao mặc dù chúng đều là các cầu thang hướng xuống hoặc lên.

3. Tam giác Penrose.

4. Trivis không thể- Tương tự "voi nhảy múa", bạn sẽ thấy mẫu thuẫn giữa số đầu ống và số mối nối với thanh ngang ở cuối. [4]

5. Đinh ba bất khả thi

Lịch sử

[sửa | sửa mã nguồn]

Một ví dụ ban đầu về một vật thể không thể đến được từ Apolinère Enameled , một quảng cáo năm 1916 do Marcel Duchamp vẽ. Nó mô tả một cô gái vẽ một khung giường với sơn trắng, và cố tình bao gồm những đường kẻ mâu thuẫn, để tạo ra một vật thể không thể. Để nhấn mạnh sự không thể thực hiện được của hình dạng, một phần của khung hình bị thiếu. Một phiên bản in 3D của hình ảnh Tam giác Reutersvärd, sự xuất hiện của nó được tạo ra bởi một viễn cảnh bắt buộc. Nghệ sĩ Thụy Điển Oscar Reutersvärd là một trong những người đầu tiên cố tình thiết kế nhiều vật thể không thể. Ông đã được gọi là "cha của con số không thể".  Năm 1934, ông vẽ tam giác Penrose, vài năm trước khi Penroses. Trong phiên bản của Reutersvärd các cạnh của tam giác được chia thành các khối. Năm 1956, Anh bác sĩ tâm thần Lionel Penrose và con trai ông, nhà toán học Roger Penrose, gửi một bài viết ngắn với tạp chí British Journal Tâm lý học mang tên "Impossible Đối tượng: một loại đặc biệt của Visual Illusion". Điều này được minh họa bằng hình tam giác Penrose và cầu thang Penrose. Bài báo nói đến Escher, tác phẩm của ông đã làm dấy lên mối quan tâm của họ về chủ đề này, nhưng không phải Reutersvärd, người mà họ không biết. Bài báo được xuất bản năm 1958.  Từ những năm 1930 trở đi, nghệ sĩ người Hà Lan MC Escher đã tạo ra nhiều bản vẽ có sự nghịch lý về quan điểm dần dần làm việc theo các đối tượng không thể.  Năm 1957, ông sản xuất bản vẽ đầu tiên của mình có chứa một đối tượng không thể thực sự: Cube với Magic Ribbons . Ông đã sản xuất nhiều bản vẽ thêm với các vật thể không thể, đôi khi với toàn bộ bản vẽ là một đối tượng không thể. Thác nước và Thung lũng Belvedere là những ví dụ điển hình về những công trình không thể xây dựng. Tác phẩm của ông đã làm nhiều để thu hút sự chú ý của công chúng đến các đối tượng không thể. Một số nghệ sĩ đương đại cũng đang thử nghiệm những con số không thể thực hiện, ví dụ như Jos de Mey, Shigeo Fukuda, Sandro del Prete, István Orosz (Utisz), Guido Moretti, Tamás F. Farkas, Mathieu Hamaekers và Kokichi Sugihara. [5]

Vật thể bất khả thi đã xây dựng được

[sửa | sửa mã nguồn]

Mặc dù vi phạm một số định luật Toán học hoặc Vật Lý nhưng nếu đứng từ một góc độ nhất định thì bạn có thể thấy được một số Vật thể bất khả thi, trong số này có tam giác Reutersvärd (tên gọi khác của tam giác Penrose) ở dạng in 3D và ở dạng điêu khắc đã được thực hiện.

dưới đây là góc nhìn của một tác phẩm điêu khắc (ở Đông Perth, Úc) từ các góc độ khác nhau. Khi khung nhìn quay, một hình tam giác Penrose dường như hình thành.góc nhìn của một tác phẩm điêu khắc (ở Đông Perth, Úc) từ các góc độ khác nhau. Khi khung nhìn quay, một hình tam giác Penrose dường như hình thành.

Do những vật có khả năng xây dựng được nhưng phải nhìn từ một góc độ bắt buộc nên người ta gọi các vật thể "không tương tác" là các vật thể mà nó xây dựng được và không thể nhìn được từ mọi phía. [6]

Chú thích

[sửa | sửa mã nguồn]

Tham khảo

[sửa | sửa mã nguồn]

Liên kết ngoài

[sửa | sửa mã nguồn]
Lấy từ “https://vi.wikipedia.org/w/index.php?title=Vật_thể_bất_khả_thi&oldid=71741557”