Tam giác Penrose
Bài viết này là một bản dịch thô từ ngôn ngữ khác. Đây có thể là kết quả của máy tính hoặc của người chưa thông thạo dịch thuật. |

Tam giác Penrose, còn được biết đến là Penrose tribar, hoặc Impossible tribar,[1] là một hình tam giác bất khả thi (Vật thể bất khả thi). Nó được tạo ra lần đầu tiên bởi nghệ sĩ người Thụy Điển Oscar Reutersvärd vào năm 1934. Nhà tâm thần học Lionel Penrose cùng với con trai là nhà toán học Roger Penrose độc lập đã phát minh ra và phổ biến nó vào những năm 1950, mô tả nó là "bất khả thi ở dạng tinh khiết nhất" của tam giác Penrose. Nó được đề cập trong các tác phẩm của nghệ sĩ M. C. Escher, với những mô tả trước đó về các vật thể bất khả thi một phần đã truyền cảm hứng cho nó.
Vật thể bất khả thi
[sửa | sửa mã nguồn]Tribar là một vật thể rắn, được tạo thành từ ba chùm hình vuông thẳng đứng, đáp ứng theo chiều ngược lại ở các góc vuông tại các đỉnh của tam giác mà chúng hình thành. Các chùm tia có thể bị vỡ do thay đổi góc nhìn, tạo thành hình khối.

Sự kết hợp các thuộc tính này không thể được thực hiện bởi bất kỳ đối tượng ba chiều nào trong Không gian Euclide. Một vật thể như vậy có thể tồn tại trong một số Euclidean đa tạp 3.[2] Ngoài ra còn có hình dạng rắn ba chiều, mỗi hình dạng, khi được nhìn từ một góc nhất định, xuất hiện giống như mô tả 2 chiều của tam giác Penrose trên trang này (ví dụ - hình ảnh liền kề mô tả tác phẩm điêu khắc ở Perth, Châu Úc). Thuật ngữ "tam giác Penrose" có thể tham chiếu đến mô tả 2 chiều hoặc chính đối tượng bất khả thi.
M.C. Escher's in thạch bản Waterfall (1961) mô tả một nguồn nước chảy trong một đường ngoằn ngoèo dọc theo các cạnh dài của hai tam giác Penrose dài, để nó kết thúc cao hơn hai tầng so với nó bắt đầu. Thác nước tạo thành các cạnh ngắn của cả hai hình tam giác, điều khiển một bánh xe nước. Escher trợ giúp chỉ ra rằng để giữ cho bánh xe quay một số nước đôi khi phải được thêm vào để bù đắp cho sự bay hơi.


Nếu một đường thẳng được tìm quanh tam giác Penrose, một Mặt Mobius 4 vòng được hình thành.[3].
Mặc dù tribar được đặt tên là một trong những vật thể bất khả thi, nhưng vẫn còn tồn tại nhiều vật thể phù hợp hơn với cùng một thể loại. Các vật thể không thể khác bao gồm cái nĩa của quỷ dữ, con voi, và vòm bất khả thi.[4]
Các đa giác Penrose khác
[sửa | sửa mã nguồn]Mặc dù có thể xây dựng tương tự với tam giác Penrose với các hình dạng khác và đa giác thông thường để tạo ra đa giác Penrose, hiệu ứng hình ảnh không nổi bật, và khi các cạnh tăng lên, vật thể dường như chỉ bị biến dạng hoặc xoắn.
-
Hình vuông Penrose
-
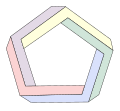
Ngũ giác Penrose
-
Lục giác Penrose
-
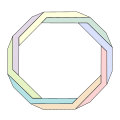
Bát giác Penrose
Xem thêm
[sửa | sửa mã nguồn]Tham khảo
[sửa | sửa mã nguồn]- ^ Pappas, T. "The Impossible Tribar." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 13, 1989.
- ^ Francis, George (1988). A topological picturebook. Springer. ISBN 0-387-96426-6. In the chapter on the Penrose tribar, Francis attributes this observation to John Stillwell.
- ^ Gardner, Martin (1978). Mathematical Games, August 1978 A Möbius band has a finite thickness, and so it is actually a twisted prism. SCIENTIFIC AMERICAN, A DIVISION OF NATURE AMERICA, INC.
- ^ Adamovic, Jan. “BrainDen.com - Impossible Objects”. BrainDen.com. Truy cập ngày 9 tháng 2 năm 2016.