Đa thức Chebyshev , được đặt theo tên nhà toán học Nga Pafnuty Chebyshev , [1] là một dãy đa thức trực giao (tiếng Anh: orthogonal polynomials), và có liên quan đến công thức de Moivre (de Moivre's formula). Có thể xác định dãy đa thức này bằng công thức truy hồi , giống như số Fibonacci và số Lucas .
Có hai loại: đa thức Chebyshev loại I (ký hiệu là Tn ) và đa thức Chebyshev loại II (ký hiệu là Un ). Chữ T được dùng để ký hiệu vì trong tiếng Pháp tên của Chebyshev viết là Tchebycheff và trong tiếng Đức là Tschebyscheff. Chữ n ký hiệu cho bậc của đa thức.
Đa thức Chebyshev đóng vai trò quan trọng trong lý thuyết gần đúng . Các nghiệm của đa thức Chebyshev loại I, còn được gọi là các điểm Chebyshev (Chebyshev node), được dùng trong đa thức nội suy . Nhờ có nó, mà sai số do hiệu ứng Runge là nhỏ nhất.
Trong phương trình vi phân , đa thức Chebyshev loại I và loại II lần lượt là nghiệm của 2 phương trình vi phân Chebyshev sau:
(
1
−
x
2
)
y
″
−
x
y
′
+
n
2
y
=
0
{\displaystyle (1-x^{2})\,y''-x\,y'+n^{2}\,y=0\,\!}
và
(
1
−
x
2
)
y
″
−
3
x
y
′
+
n
(
n
+
2
)
y
=
0
{\displaystyle (1-x^{2})\,y''-3x\,y'+n(n+2)\,y=0\,\!}
Đa thức Chebyshev loại I xác định theo công thức truy hồi :
T
0
(
x
)
=
1
T
1
(
x
)
=
x
T
n
+
1
(
x
)
=
2
x
T
n
(
x
)
−
T
n
−
1
(
x
)
.
{\displaystyle {\begin{aligned}T_{0}(x)&=1\\T_{1}(x)&=x\\T_{n+1}(x)&=2xT_{n}(x)-T_{n-1}(x).\end{aligned}}}
Công thức tổng quát quy ước của T n
∑
n
=
0
∞
T
n
(
x
)
t
n
=
1
−
t
x
1
−
2
t
x
+
t
2
.
{\displaystyle \sum _{n=0}^{\infty }T_{n}(x)t^{n}={\frac {1-tx}{1-2tx+t^{2}}}.\,\!}
Công thức mũ tổng quát
∑
n
=
0
∞
T
n
(
x
)
t
n
n
!
=
1
2
(
e
(
x
−
x
2
−
1
)
t
+
e
(
x
+
x
2
−
1
)
t
)
.
{\displaystyle \sum _{n=0}^{\infty }T_{n}(x){\frac {t^{n}}{n!}}={1 \over 2}\left(e^{(x-{\sqrt {x^{2}-1}})t}+e^{(x+{\sqrt {x^{2}-1}})t}\right).\,\!}
Đa thức Chebyshev loại II xác định theo công thức truy hồi :
U
0
(
x
)
=
1
U
1
(
x
)
=
2
x
U
n
+
1
(
x
)
=
2
x
U
n
(
x
)
−
U
n
−
1
(
x
)
.
{\displaystyle {\begin{aligned}U_{0}(x)&=1\\U_{1}(x)&=2x\\U_{n+1}(x)&=2xU_{n}(x)-U_{n-1}(x).\end{aligned}}}
Một công thức tổng quát của U n
∑
n
=
0
∞
U
n
(
x
)
t
n
=
1
1
−
2
t
x
+
t
2
.
{\displaystyle \sum _{n=0}^{\infty }U_{n}(x)t^{n}={\frac {1}{1-2tx+t^{2}}}.\,\!}
Đa thức Chebyshev loại I có thể định nghĩa bằng lượng giác :
T
n
(
x
)
=
cos
(
n
arccos
x
)
=
cosh
(
n
a
r
c
c
o
s
h
x
)
{\displaystyle T_{n}(x)=\cos(n\arccos x)=\cosh(n\,\mathrm {arccosh} \,x)\,\!}
hoặc là:
T
n
(
cos
(
ϑ
)
)
=
cos
(
n
ϑ
)
{\displaystyle T_{n}(\cos(\vartheta ))=\cos(n\vartheta )\,\!}
với n = 0, 1, 2, 3,....
Định nghĩa theo lượng giác của đa thức Chebyshev loại II :
U
n
(
cos
(
ϑ
)
)
=
sin
(
(
n
+
1
)
ϑ
)
sin
ϑ
{\displaystyle U_{n}(\cos(\vartheta ))={\frac {\sin((n+1)\vartheta )}{\sin \vartheta }}\,\!}
công thức này khá giống với nhân Dirichlet (Dirichlet kernel)
D
n
(
x
)
{\displaystyle D_{n}(x)\,\!}
D
n
(
x
)
=
sin
(
(
2
n
+
1
)
(
x
/
2
)
)
sin
(
x
/
2
)
=
U
2
n
(
cos
(
x
/
2
)
)
{\displaystyle D_{n}(x)={\frac {\sin((2n+1)(x/2))}{\sin(x/2)}}=U_{2n}(\cos(x/2))\,\!}
Dễ thấy,
cos
(
n
ϑ
)
{\displaystyle \cos(n\vartheta )}
n với
cos
(
ϑ
)
{\displaystyle \cos(\vartheta )}
cos
(
n
ϑ
)
{\displaystyle \cos(n\vartheta )}
phần thực trong công thức De Moivre (de Moivre's formula).
Từ công thức tổng quát bằng lượng giác ở trên, có thể dễ dàng chứng minh công thức truy hồi:
T
n
+
1
(
cos
(
ϑ
)
)
=
2
cos
(
ϑ
)
T
n
(
cos
(
ϑ
)
)
−
T
n
−
1
(
cos
(
ϑ
)
)
=
2
cos
(
ϑ
)
cos
(
n
ϑ
)
)
−
cos
(
(
n
−
1
)
ϑ
)
=
cos
(
(
n
+
1
)
ϑ
)
+
cos
(
(
n
−
1
)
ϑ
)
−
cos
(
(
n
−
1
)
ϑ
)
=
cos
(
(
n
+
1
)
ϑ
)
{\displaystyle T_{n+1}(\cos(\vartheta ))=2\cos(\vartheta )T_{n}(\cos(\vartheta ))-T_{n-1}(\cos(\vartheta ))=2\cos(\vartheta )\cos(n\vartheta ))-\cos((n-1)\vartheta )=\cos((n+1)\vartheta )+\cos((n-1)\vartheta )-\cos((n-1)\vartheta )=\cos((n+1)\vartheta )\,\!}
Sau đây, ta sẽ kiểm tra tính đúng đắn của định nghĩa đa thức Chebyshev theo lượng giác, với n = 0 và n = 1:
T
0
(
cos
ϑ
)
=
cos
0
ϑ
=
1
{\displaystyle T_{0}(\cos \vartheta )=\cos 0\vartheta \ =1\,\!}
và:
T
1
(
cos
ϑ
)
=
cos
ϑ
{\displaystyle T_{1}(\cos \vartheta )=\cos \vartheta \,\!}
và với đa thức Chebyshev bậc 2 và 3:
cos
(
2
ϑ
)
=
2
cos
ϑ
cos
ϑ
−
cos
0
ϑ
=
2
cos
2
ϑ
−
1
{\displaystyle \cos(2\vartheta )=2\cos \vartheta \cos \vartheta -\cos 0\vartheta =2\cos ^{2}\,\vartheta -1\,\!}
cos
(
3
ϑ
)
=
2
cos
ϑ
cos
(
2
ϑ
)
−
cos
ϑ
=
4
cos
3
ϑ
−
3
cos
ϑ
{\displaystyle \cos(3\vartheta )=2\cos \vartheta \cos(2\vartheta )-\cos \vartheta =4\cos ^{3}\,\vartheta -3\cos \vartheta \,\!}
tương tự cho các bậc cao hơn.
Một tính chất khá thú vị của đa thức Chebyshev:
T
n
(
T
m
(
x
)
)
=
T
n
⋅
m
(
x
)
.
{\displaystyle T_{n}(T_{m}(x))=T_{n\cdot m}(x).\,\!}
Mối liên hệ giữa đa thức Chebyshev và số phức : cho z = a + bi ,
z
n
=
|
z
|
n
(
cos
(
n
arccos
a
|
z
|
)
+
i
sin
(
n
arccos
a
|
z
|
)
)
=
|
z
|
n
T
n
(
a
|
z
|
)
+
i
b
|
z
|
n
−
1
U
n
−
1
(
a
|
z
|
)
.
{\displaystyle {\begin{aligned}z^{n}&=|z|^{n}\left(\cos \left(n\arccos {\frac {a}{|z|}}\right)+i\sin \left(n\arccos {\frac {a}{|z|}}\right)\right)\\&=|z|^{n}T_{n}\left({\frac {a}{|z|}}\right)+ib\ |z|^{n-1}\ U_{n-1}\left({\frac {a}{|z|}}\right).\end{aligned}}}
Trong vành R[x ] (tập hợp các đa thức với hệ số thực ),[ 1] phương trình Pell biến thể:
T
i
2
−
(
x
2
−
1
)
U
i
−
1
2
=
1
{\displaystyle T_{i}^{2}-(x^{2}-1)U_{i-1}^{2}=1\,\!}
Sử dụng kĩ thuật giải phương trình Pell có tên là "nghiệm sinh từ nghiệm nhỏ nhất", suy ra công thức tổng quát sau:
T
i
+
U
i
−
1
x
2
−
1
=
(
x
+
x
2
−
1
)
i
.
{\displaystyle T_{i}+U_{i-1}{\sqrt {x^{2}-1}}=(x+{\sqrt {x^{2}-1}})^{i}.\,\!}
Các công thức liên hệ:
T
n
(
1
−
2
x
2
)
=
(
−
1
)
n
T
2
n
(
x
)
{\displaystyle T_{n}\left(1-2x^{2}\right)=(-1)^{n}T_{2n}(x)}
và
U
n
(
1
−
2
x
2
)
x
=
(
−
1
)
n
U
2
n
+
1
(
x
)
.
{\displaystyle U_{n}\left(1-2x^{2}\right)x=(-1)^{n}U_{2n+1}(x).}
Một đa thức Cheybyshev bậc n (cả hai loại) có n nghiệm thực phân biệt, gọi là nghiệm Chebyshev , các nghiệm này đều nằm trên khoảng [−1,1]. Các nghiệm này đôi khi được gọi là các điểm nút Chebyshev (tiếng Anh: Chebyshev nodes) bởi vì chúng được dùng trong đa thức nội suy . Sử dụng định nghĩa lượng giác của đa thức Chebyshev, với
cos
(
π
2
(
2
k
+
1
)
)
=
0
{\displaystyle \cos \left({\frac {\pi }{2}}\,(2k+1)\right)=0}
ta có thể chứng minh dễ dàng các nghiệm của T n
x
k
=
cos
(
π
2
2
k
−
1
n
)
,
k
=
1
,
…
,
n
.
{\displaystyle x_{k}=\cos \left({\frac {\pi }{2}}\,{\frac {2k-1}{n}}\right),\quad k=1,\ldots ,n.}
Tương tự, các nghiệm của U n
x
k
=
cos
(
k
n
+
1
π
)
,
k
=
1
,
…
,
n
.
{\displaystyle x_{k}=\cos \left({\frac {k}{n+1}}\pi \right),\quad k=1,\ldots ,n.}
Giá trị cực đại của đa thức Chebyshev loại I trên khoảng −1 ≤ x ≤ 1 bằng 1 và giá trị cực tiểu bằng -1. Đa thức Chebyshev chỉ có 2 giá trị tới hạn , giống như đặc tính của đa thức Shabat .
Cả hai loại đa thức Chebyshev đều đạt cực trị tại 2 điểm đầu mút :
T
n
(
1
)
=
1
{\displaystyle T_{n}(1)=1\,}
T
n
(
−
1
)
=
(
−
1
)
n
{\displaystyle T_{n}(-1)=(-1)^{n}\,}
U
n
(
1
)
=
n
+
1
{\displaystyle U_{n}(1)=n+1\,}
U
n
(
−
1
)
=
(
n
+
1
)
(
−
1
)
n
.
{\displaystyle U_{n}(-1)=(n+1)(-1)^{n}.\,}
Khi đạo hàm các đa thức Chebyshev trong dạng lượng giác, ta suy ra:
d
T
n
d
x
=
n
U
n
−
1
{\displaystyle {\frac {dT_{n}}{dx}}=nU_{n-1}\,}
d
U
n
d
x
=
(
n
+
1
)
T
n
+
1
−
x
U
n
x
2
−
1
{\displaystyle {\frac {dU_{n}}{dx}}={\frac {(n+1)T_{n+1}-xU_{n}}{x^{2}-1}}\,}
d
2
T
n
d
x
2
=
n
n
T
n
−
x
U
n
−
1
x
2
−
1
=
n
(
n
+
1
)
T
n
−
U
n
x
2
−
1
.
{\displaystyle {\frac {d^{2}T_{n}}{dx^{2}}}=n{\frac {nT_{n}-xU_{n-1}}{x^{2}-1}}=n{\frac {(n+1)T_{n}-U_{n}}{x^{2}-1}}.\,}
Điểm đặc biệt của
d
2
T
n
d
x
2
{\displaystyle {\frac {d^{2}T_{n}}{dx^{2}}}}
không xác định (indeterminate form)) là x = 1 and x = -1. Tại đó
d
2
T
n
d
x
2
{\displaystyle {\frac {d^{2}T_{n}}{dx^{2}}}}
d
2
T
n
d
x
2
|
x
=
1
=
n
4
−
n
2
3
,
{\displaystyle {\frac {d^{2}T_{n}}{dx^{2}}}{\Bigg |}_{x=1}\!\!={\frac {n^{4}-n^{2}}{3}},}
d
2
T
n
d
x
2
|
x
=
−
1
=
(
−
1
)
n
n
4
−
n
2
3
.
{\displaystyle {\frac {d^{2}T_{n}}{dx^{2}}}{\Bigg |}_{x=-1}\!\!=(-1)^{n}{\frac {n^{4}-n^{2}}{3}}.}
Công thức tổng quát:
d
p
T
n
d
x
p
|
x
=
±
1
=
(
±
1
)
n
+
p
∏
k
=
0
p
−
1
n
2
−
k
2
2
k
+
1
.
{\displaystyle {\frac {d^{p}T_{n}}{dx^{p}}}{\Bigg |}_{x=\pm 1}\!\!=(\pm 1)^{n+p}\prod _{k=0}^{p-1}{\frac {n^{2}-k^{2}}{2k+1}}.}
Kết quả này có ý nghĩa rất lớn trong tìm đáp số của giá trị đặc trưng .
Tích phân của U n
∫
U
n
d
x
=
T
n
+
1
n
+
1
{\displaystyle \int U_{n}\,dx={\frac {T_{n+1}}{n+1}}\,}
Tích phân của T n
∫
T
n
d
x
=
1
2
(
T
n
+
1
n
+
1
−
T
n
−
1
n
−
1
)
=
n
T
n
+
1
n
2
−
1
−
x
T
n
n
−
1
.
{\displaystyle \int T_{n}\,dx={\frac {1}{2}}\left({\frac {T_{n+1}}{n+1}}-{\frac {T_{n-1}}{n-1}}\right)={\frac {nT_{n+1}}{n^{2}-1}}-{\frac {xT_{n}}{n-1}}.\,}
Dãy T n U n đa thức trực giao .
Cụ thể hơn, các đa thức loại I , xác định trên khoảng mở (−1,1)với mật độ (Tiếng Anh: The polynomials of the first kind are orthogonal with respect to the weight):
1
1
−
x
2
,
{\displaystyle {\frac {1}{\sqrt {1-x^{2}}}},\,\!}
∫
−
1
1
T
n
(
x
)
T
m
(
x
)
d
x
1
−
x
2
=
{
0
:
n
≠
m
π
:
n
=
m
=
0
π
/
2
:
n
=
m
≠
0
{\displaystyle \int _{-1}^{1}T_{n}(x)T_{m}(x)\,{\frac {dx}{\sqrt {1-x^{2}}}}={\begin{cases}0&:n\neq m\\\pi &:n=m=0\\\pi /2&:n=m\neq 0\end{cases}}}
Tính chất trên được chứng minh bằng cách thay
x
=
cos
(
ϑ
)
{\displaystyle x=\cos(\vartheta )}
T
n
(
cos
(
ϑ
)
)
=
cos
(
n
ϑ
)
{\displaystyle T_{n}(\cos(\vartheta ))=\cos(n\vartheta )}
Tương tự các đa thức loại II xác định trên khoảng đóng [−1,1] với mật độ (tiếng Anh: The polynomials of the second kind are orthogonal with respect to the weight):
1
−
x
2
{\displaystyle {\sqrt {1-x^{2}}}\,\!}
thì:
∫
−
1
1
U
n
(
x
)
U
m
(
x
)
1
−
x
2
d
x
=
{
0
:
n
≠
m
,
π
/
2
:
n
=
m
.
{\displaystyle \int _{-1}^{1}U_{n}(x)U_{m}(x){\sqrt {1-x^{2}}}\,dx={\begin{cases}0&:n\neq m,\\\pi /2&:n=m.\end{cases}}}
(Chú ý giá trị lượng (weight)
1
−
x
2
{\displaystyle {\sqrt {1-x^{2}}}\,\!}
phân bố nửa đường tròn Wigner (tiếng Anh: Wigner semicircle distribution).
Đa thức T n trực giao rời rạc (iếng Anh: discete orthogonality):
∑
k
=
0
N
−
1
T
i
(
x
k
)
T
j
(
x
k
)
=
{
0
:
i
≠
j
N
:
i
=
j
=
0
N
/
2
:
i
=
j
≠
0
{\displaystyle \sum _{k=0}^{N-1}{T_{i}(x_{k})T_{j}(x_{k})}={\begin{cases}0&:i\neq j\\N&:i=j=0\\N/2&:i=j\neq 0\end{cases}}\,\!}
với
x
k
{\displaystyle x_{k}}
không điểm Gauss –Lobatto thứ N của
T
N
(
x
)
{\displaystyle T_{N}(x)}
x
k
=
cos
(
π
(
k
+
1
2
)
N
)
.
{\displaystyle x_{k}=\cos \left({\frac {\pi \left(k+{\frac {1}{2}}\right)}{N}}\right).}
Với số nguyên bất kì n ≥ 1, trong số các đa thức bậc n với hệ số bậc cao nhất bằng 1, đa thức sau:
f
(
x
)
=
1
2
n
−
1
T
n
(
x
)
{\displaystyle f(x)={\frac {1}{2^{n-1}}}T_{n}(x)}
có giá trị tuyệt đối lớn nhất trên đoạn [−1, 1] nhỏ nhất.
Trong công thức trên sở dĩ nhân
1
2
n
−
1
{\displaystyle {\frac {1}{2^{n-1}}}}
T
n
(
x
)
{\displaystyle T_{n}(x)}
hệ số bậc cao nhất của đa thức
T
n
(
x
)
{\displaystyle T_{n}(x)}
2
n
−
1
{\displaystyle 2^{n-1}}
Giá trị lớn nhất đó bằng:
1
2
n
−
1
{\displaystyle {\frac {1}{2^{n-1}}}}
và |ƒ(x )| đạt giá trị lớn nhất tại n + 1
x
=
cos
k
π
n
for
0
≤
k
≤
n
.
{\displaystyle x=\cos {\frac {k\pi }{n}}{\text{ for }}0\leq k\leq n.}
Chứng minh
Giả sử tồn tại đa thức
w
n
(
x
)
{\displaystyle w_{n}(x)}
n với hệ số bậc cao nhất bằng 1, và giá trị tuyệt đối lớn nhất trên [−1, 1] nhỏ hơn
1
2
n
−
1
{\displaystyle {\frac {1}{2^{n-1}}}}
Xét đa thức sau:
f
n
(
x
)
=
1
2
n
−
1
T
n
(
x
)
−
w
n
(
x
)
{\displaystyle f_{n}(x)={\frac {1}{2^{n-1}}}T_{n}(x)-w_{n}(x)}
đa thức này có bậc nhỏ thua n.
Do giả thiết, tại mỗi điểm
T
n
(
x
)
{\displaystyle T_{n}(x)}
±
1
{\displaystyle \pm 1}
|
w
n
(
x
)
|
<
|
1
2
n
−
1
T
n
(
x
)
|
{\displaystyle |w_{n}(x)|<|{\frac {1}{2^{n-1}}}T_{n}(x)|}
f
n
(
x
)
>
0
for
x
=
cos
2
k
π
n
với
0
≤
2
k
≤
n
{\displaystyle f_{n}(x)>0{\text{ for }}x=\cos {\frac {2k\pi }{n}}{\text{ với }}0\leq 2k\leq n}
f
n
(
x
)
<
0
for
x
=
cos
(
2
k
+
1
)
π
n
với
0
≤
2
k
+
1
≤
n
{\displaystyle f_{n}(x)<0{\text{ for }}x=\cos {\frac {(2k+1)\pi }{n}}{\text{ với }}0\leq 2k+1\leq n}
Như vậy
f
n
(
x
)
{\displaystyle f_{n}(x)}
nghiệm trên n khoảng
(
0
,
P
i
n
)
,
(
P
i
n
,
2
P
i
n
)
,
…
(
(
n
−
1
)
P
i
n
,
n
P
i
n
)
{\displaystyle (0,{\frac {Pi}{n}}),({\frac {Pi}{n}},{\frac {2Pi}{n}}),\ldots ({\frac {(n-1)Pi}{n}},{\frac {nPi}{n}})}
f
n
(
x
)
{\displaystyle f_{n}(x)}
Suy ra điều giả sử là sai. ta có điều phải chứng minh.
Đa thức Chebyshev là trường hợp đặc biệt của Jacobi và đa thức Gegenbauer ,
T
n
(
x
)
=
1
(
n
−
1
2
n
)
P
n
−
1
2
,
−
1
2
(
x
)
=
n
2
C
n
0
(
x
)
,
{\displaystyle T_{n}(x)={\frac {1}{n-{\frac {1}{2}} \choose n}}P_{n}^{-{\frac {1}{2}},-{\frac {1}{2}}}(x)={\frac {n}{2}}C_{n}^{0}(x),}
U
n
(
x
)
=
1
2
(
n
+
1
2
n
)
P
n
1
2
,
1
2
(
x
)
=
C
n
1
(
x
)
.
{\displaystyle U_{n}(x)={\frac {1}{2{n+{\frac {1}{2}} \choose n}}}P_{n}^{{\frac {1}{2}},{\frac {1}{2}}}(x)=C_{n}^{1}(x).}
Đa thức Chebyshev là trường hợp đặc biệt của đa thức Gegenbauer , đến lượt mình đa thức Gegenbauer lại là trường hợp đặc biệt của Jacobi .
Với số nguyên n bất kì, T n x ) và U n x ) đều là đa thức bậc n .
Nếu n chẵn thì T n x ) và U n x ) là hàm chẵn, nghĩa là chỉ có các hệ số tương ứng với bậc chẵn là khác 0.
Ví dụ:
T
0
(
x
)
=
1
{\displaystyle T_{0}(x)=1\,}
T
2
(
x
)
=
2
x
2
−
1
{\displaystyle T_{2}(x)=2x^{2}-1\,}
T
4
(
x
)
=
8
x
4
−
8
x
2
+
1
{\displaystyle T_{4}(x)=8x^{4}-8x^{2}+1\,}
U
0
(
x
)
=
1
{\displaystyle U_{0}(x)=1\,}
U
2
(
x
)
=
4
x
2
−
1
{\displaystyle U_{2}(x)=4x^{2}-1\,}
U
4
(
x
)
=
16
x
4
−
12
x
2
+
1
{\displaystyle U_{4}(x)=16x^{4}-12x^{2}+1\,}
Nếu n lẻ thì T n x ) và U n x ) là hàm lẻ, nghĩa là chỉ có các hệ số tương ứng với bậc lẻ là khác 0.
Ví dụ:
T
1
(
x
)
=
x
{\displaystyle T_{1}(x)=x\,}
T
3
(
x
)
=
4
x
3
−
3
x
{\displaystyle T_{3}(x)=4x^{3}-3x\,}
U
1
(
x
)
=
2
x
{\displaystyle U_{1}(x)=2x\,}
U
3
(
x
)
=
8
x
3
−
4
x
{\displaystyle U_{3}(x)=8x^{3}-4x\,}
Hệ số bậc cao nhất của T n 2n − 1 if 1 ≤ n , và 1 tương ứng với bậc bằng 0.
T n đường cong Lissajous curve với tần số tỉ lệ (tiếng Anh: frequency ratio) là n .
Một số dãy đa thức khác, ví dụ đa thức Lucas (L n đa thức Dickson (D n đa thức Fibonacci (F n T n U n
Đa thức Chebyshev loại I thỏa mãn công thức truy hồi sau:
T
j
(
x
)
T
k
(
x
)
=
1
2
(
T
j
+
k
(
x
)
+
T
|
j
−
k
|
(
x
)
)
,
∀
j
,
k
≥
0
,
{\displaystyle T_{j}(x)T_{k}(x)={\frac {1}{2}}\left(T_{j+k}(x)+T_{|j-k|}(x)\right),\quad \forall j,k\geq 0,\,}
với mọi j và k.
Đối với đa thức Chebyshev loại II là:
U
j
(
x
)
U
k
(
x
)
=
(
U
j
+
k
(
x
)
+
U
|
j
−
k
|
(
x
)
)
,
∀
j
≠
0
,
k
≠
0
{\displaystyle U_{j}(x)U_{k}(x)=\left(U_{j+k}(x)+U_{|j-k|}(x)\right),\quad \forall j\neq 0,k\neq 0}
Từ công thức:
T
n
(
cos
θ
)
=
cos
(
n
θ
)
{\displaystyle T_{n}(\cos \theta )=\cos(n\theta )}
suy ra công thức sau:
T
2
n
+
1
(
sin
θ
)
=
(
−
1
)
n
sin
(
(
2
n
+
1
)
θ
)
{\displaystyle T_{2n+1}(\sin \theta )=(-1)^{n}\sin((2n+1)\theta )}
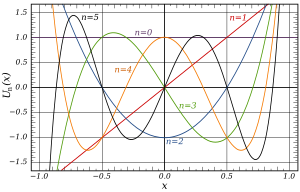
Các đa thức Chebyshev loại I đầu tiên trong khoảng −1 < x < 1 : Đồ thị của T 0 T 1 T 2 T 3 T 4 T 5 Các đa thức Chebyshev loại I đầu tiên:
T
0
(
x
)
=
1
{\displaystyle T_{0}(x)=1\,}
T
1
(
x
)
=
x
{\displaystyle T_{1}(x)=x\,}
T
2
(
x
)
=
2
x
2
−
1
{\displaystyle T_{2}(x)=2x^{2}-1\,}
T
3
(
x
)
=
4
x
3
−
3
x
{\displaystyle T_{3}(x)=4x^{3}-3x\,}
T
4
(
x
)
=
8
x
4
−
8
x
2
+
1
{\displaystyle T_{4}(x)=8x^{4}-8x^{2}+1\,}
T
5
(
x
)
=
16
x
5
−
20
x
3
+
5
x
{\displaystyle T_{5}(x)=16x^{5}-20x^{3}+5x\,}
T
6
(
x
)
=
32
x
6
−
48
x
4
+
18
x
2
−
1
{\displaystyle T_{6}(x)=32x^{6}-48x^{4}+18x^{2}-1\,}
T
7
(
x
)
=
64
x
7
−
112
x
5
+
56
x
3
−
7
x
{\displaystyle T_{7}(x)=64x^{7}-112x^{5}+56x^{3}-7x\,}
T
8
(
x
)
=
128
x
8
−
256
x
6
+
160
x
4
−
32
x
2
+
1
{\displaystyle T_{8}(x)=128x^{8}-256x^{6}+160x^{4}-32x^{2}+1\,}
T
9
(
x
)
=
256
x
9
−
576
x
7
+
432
x
5
−
120
x
3
+
9
x
.
{\displaystyle T_{9}(x)=256x^{9}-576x^{7}+432x^{5}-120x^{3}+9x.\,}
Các đa thức Chebyshev loại II đầu tiên trong khoảng −1 < x < 1: Đồ thị của U 0 U 1 U 2 U 3 U 4 U 5 U n n + 1U n n + 1)(−1)n Các đa thức Chebyshev loại II đầu tiên:
U
0
(
x
)
=
1
{\displaystyle U_{0}(x)=1\,}
U
1
(
x
)
=
2
x
{\displaystyle U_{1}(x)=2x\,}
U
2
(
x
)
=
4
x
2
−
1
{\displaystyle U_{2}(x)=4x^{2}-1\,}
U
3
(
x
)
=
8
x
3
−
4
x
{\displaystyle U_{3}(x)=8x^{3}-4x\,}
U
4
(
x
)
=
16
x
4
−
12
x
2
+
1
{\displaystyle U_{4}(x)=16x^{4}-12x^{2}+1\,}
U
5
(
x
)
=
32
x
5
−
32
x
3
+
6
x
{\displaystyle U_{5}(x)=32x^{5}-32x^{3}+6x\,}
U
6
(
x
)
=
64
x
6
−
80
x
4
+
24
x
2
−
1
{\displaystyle U_{6}(x)=64x^{6}-80x^{4}+24x^{2}-1\,}
U
7
(
x
)
=
128
x
7
−
192
x
5
+
80
x
3
−
8
x
{\displaystyle U_{7}(x)=128x^{7}-192x^{5}+80x^{3}-8x\,}
U
8
(
x
)
=
256
x
8
−
448
x
6
+
240
x
4
−
40
x
2
+
1
{\displaystyle U_{8}(x)=256x^{8}-448x^{6}+240x^{4}-40x^{2}+1\,}
U
9
(
x
)
=
512
x
9
−
1024
x
7
+
672
x
5
−
160
x
3
+
10
x
.
{\displaystyle U_{9}(x)=512x^{9}-1024x^{7}+672x^{5}-160x^{3}+10x.\,}
Bản mẫu:Abramowitz Stegun ref Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), “Orthogonal Polynomials” , trong Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (biên tập), NIST Handbook of Mathematical Functions ISBN 978-0521192255 MR 2723248 Bản mẫu:Eom 

































![{\displaystyle =-4x^{2}(-1)^{n}T_{2n}(x)+(-1)^{n}.[T_{2n}(x)+T_{2n-2}(x)]+(-1)^{n}.T_{2n}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8463d8837535b4eea2c69c5df610ebd3944b099f)

![{\displaystyle =-2x(-1)^{n}[2xT_{2n}(x)-T_{2n-1}(x)]+(-1)^{n}.T_{2n}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7b6eb58c05eb4ad8fc5591816fe2d0c40e1ccf4)

![{\displaystyle =(-1)^{n+1}[2xT_{2n+1}(x)-T_{2n}(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffb0f67a54de76fcb95a36d41a6eeab6acea2f38)











































































