Bước tới nội dung

Tiến động cận điểm

Bách khoa toàn thư mở Wikipedia
Bài này viết về sự quay của bản thân quỹ đạo của một thiên thể. Đối với tiến động của trục quay của thiên thể và biến thiên trong độ nghiêng quỹ đạo, xem Tiến động trục quay.
Đối với tiến động của các điểm nút quỹ đạo hay biến thiên kinh độ của điểm nút lên, xem Tiến động điểm nút.
Mỗi hành tinh quay xung quanh Mặt Trời chuyển động trên một quỹ đạo elip quay rất chậm theo thời gian (tiến động cận điểm). Hình này minh họa một sự tiến động điểm cận nhật dương, với trục cận viễn của quỹ đạo quay theo cùng chiều chuyển động quỹ đạo của chính thiên thể. Độ lệch tâm của quỹ đạo elip và tốc độ tiến động của quỹ đạo đã được phóng đại để dễ nhận thấy. Phần lớn quỹ đạo trong hệ Mặt Trời có độ lệch tâm thấp hơn rất nhiều và tiến động với tốc độ cũng rất thấp hơn, do đó chúng khá gần với quỹ đạo tròn và tĩnh.
Sáu tham số quỹ đạo chính. Đường cận viễn được tô màu xanh lam, và acgumen của cận điểm được ký hiệu bởi ω. Tiến động cận điểm là tốc độ thay đổi của ω theo thời gian, dω/dt.
Hoạt ảnh mô tả quỹ đạo của Mặt Trăng quanh Trái Đất - nhìn từ phía cực.       Mặt Trăng ·       Trái Đất

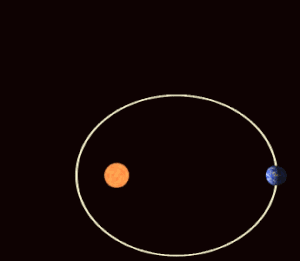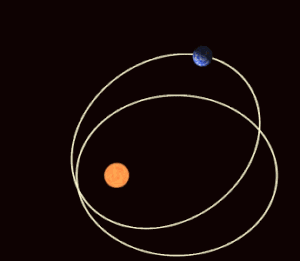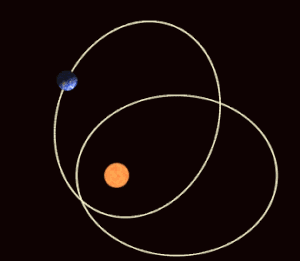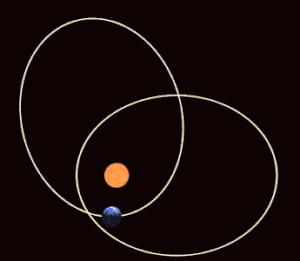
Trong cơ học thiên thể, tiến động cận điểm[1] là sự tiến động (sự quay rất chậm) của đường thẳng nối hai củng điểm (đường cận viễn hay củng tuyến) của quỹ đạo của một thiên thể. Các củng điểm (apsis) là hai điểm trên quỹ đạo gần nhất (cận điểm) và xa nhất (viễn điểm) so với thiên thể trung tâm. Tiến động cận điểm là đạo hàm bậc nhất theo thời gian của acgumen của cận điểm, một trong sáu tham số quỹ đạo chính của một quỹ đạo. Tiến động cận điểm được coi là theo chiều dương nếu trục cận viễn của thiên thể quay cùng chiều với chuyển động quỹ đạo. Chu kỳ củng điểm là khoảng thời gian cần thiết để một quỹ đạo tiến động 360°.[2]

Lịch sử

[sửa | sửa mã nguồn]

Nhà thiên văn Hy Lạp cổ đại Hipparchus đã chú ý tới tiến động cận điểm của quỹ đạo Mặt Trăng;[3] và nó đã được tinh chỉnh trong cỗ máy Antikythera (có niên đại khoảng 80 TCN) với giá trị rất chính xác là 8,88 năm mỗi chu kỳ, chính xác tới trong khoảng 0,34% so với các phép đo hiện đại.[4] Sự tiến động cận điểm của quỹ đạo quanh Mặt Trời của Trái Đất được phát hiện vào thế kỷ thứ 11 bởi al-Zarqālī.[5] Tiến động cận điểm của Mặt Trăng không được giải thích trong Almagest của Claudius Ptolemy, và nhóm các tiến động này, kết quả của rất nhiều ảnh hưởng khác nhau, vẫn còn khó giải thích được cho đến thế kỷ thứ 20 khi trường hợp cuối cùng, tiến động của quỹ đạo Sao Thủy được mô hình hóa chính xác.

Tính toán

[sửa | sửa mã nguồn]

Nhiều nhân tố khác nhau có thể dẫn tới tiến động của cận điểm, chẳng hạn hấp dẫn tương đối rộng, các mômen tứ cực sao, biến dạng thủy triều tương hỗ của sao-hành tinh, và ảnh hưởng nhiễu loạn từ các hành tinh khác.[6]

Đối với Sao Thủy, tốc độ tiến động điểm cận nhật do các hiệu ứng tương đối rộng là 43″ (giây cung) mỗi thế kỷ. Trong khi đó tiến động do nhiễu loạn hấp dẫn từ các hành tinh khác trong hệ Mặt Trời là 532″ mỗi thế kỷ, còn độ cầu dẹt của Mặt Trời (mômen tứ cực) gây ra đóng góp rất nhỏ 0,025″ mỗi thế kỷ.[7][8]

Theo cơ học cổ điển, nếu các ngôi sao và hành tinh đều được coi là các khối hoàn toàn hình cầu thì chúng sẽ tuân theo quy luật khoảng cách bình phương nghịch đảo 1/r2 đơn giản, liên hệ lực theo khoảng cách và do đó sẽ thực hiện quỹ đạo elip kín theo định lý Bertrand. Các hiệu ứng do khối lượng không phải là hình cầu được gây ra bởi tác động của thế bên ngoài: thế ly tâm của các thiên thể quay gây ra sự dẹt giữa các cực và lực hấp dẫn của một khối lượng gần đó sẽ nâng phình thủy triều. Biến dạng phình do sự quay và các phình thủy triều tổng cộng tạo ra các trường tứ cực hấp dẫn (1/r3), dẫn đến tiến động của quỹ đạo.

Đối với tiến động cận điểm của các thiên thể Sao Mộc rất nóng và cô lập, thành phần phình thủy triều của hành tinh chiếm phần lớn nhất và hơn một bậc độ lớn so với ảnh hưởng của hiệu ứng tương đối rộng và mômen tứ cực sao. Kết quả xấp xỉ của độ phình thủy triều rất hữu ích để tìm hiểu cấu trúc bên trong của các hành tinh như vậy. Với các hành tinh có chu kỳ quỹ đạo ngắn nhất, cấu trúc trong của hành tinh gây ra tiến động khoảng vài độ mỗi năm, chẳng hạn lên tới 19,9° mỗi năm đối với WASP-12b.[9][10]

Thuyết tương đối rộng

[sửa | sửa mã nguồn]

Sự tiến động cận điểm của hành tinh Sao Thủy đã được chú ý bởi nhà thiên văn Urbain Le Verrier người Pháp vào khoảng giữa thế kỷ 19 và có thể được giải thích bởi thuyết tương đối rộng của Einstein.

Einstein đã chứng tỏ rằng đối với một hành tinh, với bán trục lớn của quỹ đạo elip là a, độ lệch tâm quỹ đạo e, và chu kỳ quỹ đạo T, tiến động cận điểm do các hiệu ứng tương đối trong một chu kỳ quay bằng đơn vị radians là

trong đó c là tốc độ ánh sáng trong chân không.[11] Trong trường hợp của Sao Thủy, bán trục lớn là khoảng 579×1010 m, độ lệch tâm của quỹ đạo này là 0,206 và chu kỳ quay quanh Mặt Trời là 87,97 ngày hay 76×106 s. Từ những giá trị trên và tốc độ ánh sáng (bằng ~3×108 m/s), có thể tính được tiến động cận điểm trong một chu kỳ quỹ đạo là ε = 5028×10−7 radian (288×10−5 độ hay 0,104″). Trong thời gian 100 năm, Sao Thủy hoàn thành xấp xỉ 415 vòng quay quanh Mặt Trời, và do đó trong thời gian ấy, tiến động của điểm cận nhật do hiệu ứng tương đối là xấp xỉ 43″, khớp gần đúng với những giá trị quan trắc được mà trước đó chưa được giải thích.

Ảnh hưởng khí hậu dài hạn

[sửa | sửa mã nguồn]

Do tiến động cận điểm của Trái Đất, acgumen của điểm cận nhật tăng nhưng rất chậm; phải mất 112000 năm để quỹ đạo elip hoàn thành một vòng quay tiến động so với các sao cố định.[12] Trục cực của Trái Đất, kéo theo đó là các điểm chí và điểm phân, cũng tiến động với chu kỳ khoảng 26000 năm so với các sao cố định. Hai dạng 'tiến động' này kết hợp sao cho sau khoảng từ 20800 tới 29000 năm (trung bình 23000 năm) quỹ đạo elip sẽ quay một vòng tương đối với điểm xuân phân, tức là để điểm cận nhật quay trở lại ngày tháng trước đó (nếu cho một lịch ghi chép các mùa một cách hoàn hảo).[13]

Tác động tương hỗ này của các chu kỳ cận điểm và chu kỳ chí tuyến có ảnh hưởng quan trọng tới các biến đổi khí hậu dài hạn trên Trái Đất, được gọi là các chu kỳ Milankovitch. Một chu kỳ tương tự cũng đã được biết đến trên Sao Hỏa.

Tiến động cận điểm có ảnh hưởng đến độ dài và thời gian của các mùa, và tác động này càng rõ rệt nếu độ lệch tâm quỹ đạo càng lớn, tức là các khoảng cách cận nhật và viễn nhật càng chênh lệch. Do định hướng quỹ đạo Trái Đất thay đổi, thời điểm bắt đầu của các mùa sẽ sớm hơn mỗi năm tuy rất chậm. Bởi chuyển động không đều trên quỹ đạo của Trái Đất, một mùa sẽ dài hơn nếu nó xảy ra tại phía xa của quỹ đạo, và ngược lại. Ngoài ra, nếu điểm cận nhật xảy ra trong mùa hạ đối với một bán cầu của Trái Đất, độ nghiêng trục và độ lệch tâm quỹ đạo có tác động tổng hợp tới sự tăng lượng bức xạ Mặt Trời vào mùa hạ của bán cầu đó.[14]

Các hiệu ứng của tiến động cận điểm đến mùa màng, với độ lệch tâm và điểm (viễn hay) cận nhật trên quỹ đạo, được phóng đại lên một chút để dễ thấy hơn. Các mùa màng hiển thị đây là ở bắc bán cầu, tại bất cứ thời điểm nào đó trên quỹ đạo, và ở nam bán cầu các mùa sẽ đảo ngược lại. Một vài hiệu ứng khí hậu khác sẽ tiếp theo, phần lớn là vì Nam Bán Cầu có nhiều đại dương hơn.

Xem thêm

[sửa | sửa mã nguồn]

Tham khảo

[sửa | sửa mã nguồn]
  1. ^ Bowler, M. G. (2010). “Apsidal advance in SS 433?”. Astronomy and Astrophysics. 510 (1): A28. arXiv:0910.3536. Bibcode:2010A&A...510A..28B. doi:10.1051/0004-6361/200913471. S2CID 119289498.
  2. ^ Hilditch, R. W. (2001). An Introduction to Close Binary Stars. Cambridge astrophysics series. Cambridge University Press. tr. 132. ISBN 9780521798006.
  3. ^ Jones, A., Alexander (tháng 9 năm 1991). “The Adaptation of Babylonian Methods in Greek Numerical Astronomy” (PDF). Isis. 82 (3): 440–453. Bibcode:1991Isis...82..441J. doi:10.1086/355836. S2CID 92988054. Bản gốc (PDF) lưu trữ ngày 4 tháng 3 năm 2016. Truy cập ngày 6 tháng 6 năm 2022.
  4. ^ Freeth, Tony; Bitsakis, Yanis; Moussas, Xenophon; Seiradakis, John. H.; Tselikas, A.; Mangou, H.; Zafeiropoulou, M.; Hadland, R.; và đồng nghiệp (30 tháng 11 năm 2006). “Decoding the ancient Greek astronomical calculator known as the Antikythera Mechanism” (PDF). Nature. 444 Supplement (7119): 587–91. Bibcode:2006Natur.444..587F. doi:10.1038/nature05357. PMID 17136087. S2CID 4424998. Bản gốc (PDF) lưu trữ ngày 20 tháng 7 năm 2015. Truy cập ngày 20 tháng 5 năm 2014.
  5. ^ Toomer, G. J. (1969), “The Solar Theory of az-Zarqāl: A History of Errors”, Centaurus, 14 (1): 306–336, Bibcode:1969Cent...14..306T, doi:10.1111/j.1600-0498.1969.tb00146.x, at pp. 314–317.
  6. ^ David M. Kipping (8 tháng 8 năm 2011). The Transits of Extrasolar Planets with Moons. Springer. tr. 84–. ISBN 978-3-642-22269-6. Truy cập ngày 27 tháng 8 năm 2013.
  7. ^ Kane, S. R.; Horner, J.; von Braun, K. (2012). “Cyclic Transit Probabilities of Long-period Eccentric Planets due to Periastron Precession”. The Astrophysical Journal. 757 (1): 105. arXiv:1208.4115. Bibcode:2012ApJ...757..105K. doi:10.1088/0004-637x/757/1/105. S2CID 54193207.
  8. ^ Richard Fitzpatrick (30 tháng 6 năm 2012). An Introduction to Celestial Mechanics. Cambridge University Press. tr. 69. ISBN 978-1-107-02381-9. Truy cập ngày 26 tháng 8 năm 2013.
  9. ^ Ragozzine, D.; Wolf, A. S. (2009). “Probing the interiors of very hot Jupiters using transit light curves”. The Astrophysical Journal. 698 (2): 1778–1794. arXiv:0807.2856. Bibcode:2009ApJ...698.1778R. doi:10.1088/0004-637x/698/2/1778. S2CID 29915528.
  10. ^ Michael Perryman (26 tháng 5 năm 2011). The Exoplanet Handbook. Cambridge University Press. tr. 133–. ISBN 978-1-139-49851-7. Truy cập ngày 26 tháng 8 năm 2013.
  11. ^ Hawking, Stephen (2002). On the Shoulders of Giants : the Great Works of Physics and Astronomy. Philadelphia, Pennsylvania, USA: Running Press. tr. der Physik. ISBN 0-7624-1348-4.
  12. ^ van den Heuvel, E. P. J. (1966). “On the Precession as a Cause of Pleistocene Variations of the Atlantic Ocean Water Temperatures”. Geophysical Journal International. 11 (3): 323–336. Bibcode:1966GeoJ...11..323V. doi:10.1111/j.1365-246X.1966.tb03086.x.
  13. ^ The Seasons and the Earth's Orbit, United States Naval Observatory, Bản gốc lưu trữ ngày 2 tháng 8 năm 2013, truy cập ngày 16 tháng 8 năm 2013
  14. ^ David Parry Rubincam (2004). “The Precession Index, A Nonlinear Energy Balance Model, And Seversmith Psychroterms” (PDF). NASA Technical Report. Greenbelt (MD).
Lấy từ “https://vi.wikipedia.org/w/index.php?title=Tiến_động_cận_điểm&oldid=71783275”