Tỷ lệ vàng trong hình học

Tỷ lệ vàng trên một đoạn thẳng

Tỷ lệ vàng trong hình học được xác định nếu một đoạn thẳng chia phần theo tỷ lệ vàng: Tỷ số giữa tổng hai đoạn thẳng a + b với đoạn thẳng dài hơn a bằng tỷ số giữa a với đoạn thẳng ngắn hơn b. Tỷ lệ vàng thường được ký hiệu bằng ký tự $\varphi$ (phi) trong bảng chữ cái Hy Lạp nhằm tưởng nhớ đến Phidias, nhà điêu khắc đã xây dựng nên đền Parthenon.

Như hình bên phải, tỷ lệ vàng được biểu diễn như sau:

${\frac {a+b}{a}}={\frac {a}{b}}=\varphi$

Phương trình này có nghiệm đại số xác định là một số vô tỷ:

$\varphi ={\frac {1+{\sqrt {5}}}{2}}\approx 1.61803\,39887\ldots \,$

Trong bài viết này sẽ trình bày một số cách chia tỷ số vàng trong lĩnh vực hình học phẳng.

Chia tỷ lệ vàng trên đoạn thẳng

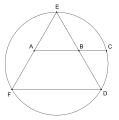
Xây dựng trên tam giác đều và tam giác vuông cân

• Cách dựng tỉ số vàng của George Phillips Odom: Cho tam giác A,B là trung điểm của các cạnh EF, ED của tam giác đều DEF. Khi đó đường thẳng AB cắt đường tròn ngoại tiếp tam giác DEF tại C ta có tỉ lệ vàng sau: ${\tfrac {AB}{BC}}=\varphi$
• Cho tam giác vuông cân ABC tại A, lấy G, F trên cạnh AC, AB sao cho $AG=AF={\tfrac {AB}{3}}$ khi đó đường thẳng GF sẽ cắt đường tròn ngoại tiếp tam giác ABC tại hai điểm H, E thỏa mãn ${\tfrac {GF}{FE}}=\varphi$.
• Cho tam giác đều ABC, lấy D, E trên cạnh AC, AB sao cho $CD=BE={\tfrac {BC}{4}}$ khi đó đường tròn ngoại tiếp tam giác ADE sẽ cắt cạnh đáy BC tại hai điểm FG, với ${\tfrac {FG}{GB}}=\varphi$
• Cho tam giác vuông cân ABC tại A, lấy D, E trên cạnh AC, AB sao cho $AD=AE={\tfrac {3}{5}}AB$ khi đó đường tròn ngoại tiếp tam giác ADE sẽ cắt cạnh đáy BC tại hai điểm H, G, với ${\tfrac {HG}{GC}}=\varphi$.

• 
  Đường trung bình của tam giác đều cắt đường tròn ngoại tiếp xác định tỉ số vàng, cách xác định bởi George Phillips Odom
• 
  Cách chia tỉ lệ vàng trong tam giác đều bởi Đào Thanh Oai
• 
  Cách chia tỉ lệ vàng trong tam giác vuông cân bởi Trần Quang Hùng
• 
  Cách chia tỉ lệ vàng trong tam giác vuông cân bởi Đào Thanh Oai
• 
  Ngôi sao năm cánh và tỉ lệ vàng

Xây dựng trên ngôi sao năm cánh

Ngôi sao năm cánh trong hình trên có các đoạn được tô màu đỏ, xanh lá cây, xanh nước biển, tím để phân biệt những đoạn có độ dài khác nhau. Chiều dài của bốn đoạn thẳng đó đó xác định tỷ lệ vàng. Đỏ/Xanh lá cây=Xanh lá cây/Xanh nước biển=Xanh nước biển/Tím=Tỉ lệ vàng.

Một số đa giác đặc biệt liên quan đến tỷ số vàng

• 
  Tam giác vàng
• 
  Tam giác Kepler
• 
  Hình thoi vàng.
• 
  Hình chữ nhật vàng
• 
  Cách dựng hình chữ nhật vàng

Tam giác tỷ lệ vàng

Một tam giác tỷ lệ vàng cũng còn có tên tam giác vàng, là một tam giác cân với chiều dài cạnh bên chia cho chiều dài cạnh đáy bằng tỷ lệ vàng

${a \over b}=\varphi ={1+{\sqrt {5}} \over 2}.$

$\theta =\cos ^{-1}\left({\varphi \over 2}\right)={\pi \over 5}=36^{\circ }.$

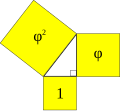
Tam giác Kepler

Tam giác Kepler là một tam giác vuông đặc biệt với diện tích của các hình vuông có cạnh bằng các cạnh của tam giác đó (xem hình trên) thỏa mãn tỷ lệ $1:\varphi :\varphi ^{2}$

Hình thoi vàng

Hình thoi tỷ lệ vàng là một hình thoi có tỷ lệ các đường chéo là tỷ lệ vàng , ${\frac {p}{q}}=\varphi \!$.

Hình chữ nhật vàng

Phương pháp của Le Corbusier: Vẽ một hình vuông rồi chia đôi hình vuông đó ra, rồi lấy trung điểm của cạnh vuông làm tâm vẽ một cung tròn có bán kính bằng đường chéo của hình chữ nhật nửa hình vuông, sẽ giúp ta kéo dài cạnh vuông ra thành một chiều dài cân đối Tỷ Lệ Vàng với cạnh vuông. Ngoài ra ta còn có diện tích của hình vuông tỷ lệ với diện tích của hình chữ nhật tỷ lệ vàng mới hình thành bởi cạnh kéo dài.

Phương pháp Le Corbusier xem như có tính tổng hợp các phương pháp có trước đó, cho nên khá phong phú, toàn diện: một chiều dài hoặc một diện tích có sẵn, ta có thể tìm ra các thành phần lớn hơn và nhỏ hơn mà cân đối với nhau.

Xem thêm

• Tỷ lệ vàng
• Tỷ lệ bạc
• Tam giác vuông đặc biệt
• Tam giác cân

Liên kết ngoài

• Golden Ratio in Geometry tại Cut-The-Knot
• Two-dimensional Geometry and the Golden section or Fascinating Flat Facts about Phi