Tối ưu hóa tô pô
Tối ưu hóa cấu trúc (Topology Optimization-TO) là phương pháp tối ưu hóa thiết kế cơ khí bằng phương pháp toán học. Mục tiêu là tìm phân bố vật liệu tối ưu cho thiết kế ban đầu để giảm khối lượng nhưng vẫn đảm bảo được ứng xử của cơ hệ như điều kiện bền, độ cứng, độ ổn định ... Ở đây thiết kế ban đầu có chịu điều kiện biên và tải trọng cho trước. Để tìm ứng xử của cơ hệ trong phương pháp TO, chúng ta sử dụng phương pháp phần tử hữu hạn [FEM].
Nghiệm thiết kế tối ưu của cơ hệ ban đầu được tìm dựa trên 02 nhóm giải thuật tối ưu:
- Giải thuật tối ưu dựa trên đạo hàm của hàm mục tiêu và ràng buộc (Gradient-based optimization): Method of Moving Asymptotes (MMA), Sequential Quadratic Programming (SQP)...
- Giải thuật tối ưu không dùng đạo hàm (None-gradient based optimization): Genetic Algorithm (GA), Differential Evolution (DE) ...
Định nghĩa bài toán
[sửa | sửa mã nguồn]Bài toán tối ưu hóa cấu trúc (TO) được viết dưới dạng bài toán tối ưu như sau:
Báo cáo vấn đề bao gồm:
- Một hàm mục tiêu . Hàm này đại diện cho một lượng được cực tiểu hóa để có hiệu suất tốt nhất. Hàm mục tiêu phổ biến nhất là hàm tuân thủ, trong đó tối thiểu hóa tuân thủ \ dẫn đến tối đa hóa độ cứng của một cấu trúc.
- Sự phân bố vật liệu là một biến vấn đề. Điều này được mô tả bởi mật độ của vật liệu tại mỗi vị trí . Có vật liệu, được biểu thị bằng 1 hoặc không có, được biểu thị bằng 0.
- Ràng buộc một đặc tính mà giải pháp phải thỏa mãn. Ví dụ là lượng vật liệu tối đa được phân phối (hạn chế về khối lượng) hoặc các giá trị ứng suất tối đa.
Đánh giá thường bao gồm việc giải phương trình vi phân. Điều này thường được thực hiện bằng phương pháp phần tử hữu hạn vì các phương trình này không có giải pháp phân tích đã biết.
Phương pháp triển khai
[sửa | sửa mã nguồn]Có nhiều phương pháp triển khai khác nhau đã được sử dụng để giải quyết các vấn đề về TO.
Rời rạc
[sửa | sửa mã nguồn]Giải quyết các vấn đề TO rời rạc được thực hiện bằng cách cụ thể hoá miền thiết kế thành các phần tử hữu hạn. Mật độ vật liệu bên trong các yếu tố này sau đó được coi là các biến vấn đề. Trong trường hợp này, mật độ vật chất cho biết sự hiện diện của vật liệu, trong khi 0 cho biết sự vắng mặt của vật liệu. Do độ phức tạp topo có thể đạt được của thiết kế phụ thuộc vào số lượng các phần tử, nên một lượng lớn được ưu tiên. Một lượng lớn các phần tử hữu hạn làm tăng độ phức tạp topo có thể đạt được, nhưng sẽ dẫn đến chi phí. Thứ nhất, giải quyết hệ thống FEM trở nên đắt hơn. Thứ hai, chưa có các thuật toán có thể xử lý một số lượng lớn (vài nghìn phần tử không phải là hiếm) biến rời rạc với nhiều ràng buộc. Hơn nữa, chúng nhạy cảm không chính xác với các biến thể tham số.[1] Trong các tài liệu, vấn đề lên đến 30000 biến đã được báo cáo [2]
Giải quyết vấn đề với các biến liên tục
[sửa | sửa mã nguồn]Những phức tạp đã nêu trước đây với việc giải quyết vấn đề TO bằng cách sử dụng các biến nhị phân đã khiến cộng đồng tìm kiếm các tùy chọn khác. Một là mô hình hóa mật độ với các biến liên tục. Mật độ vật liệu bây giờ cũng có thể đạt được giá trị giữa số 0 và 1. Các thuật toán dựa trên Gradient xử lý một lượng lớn các biến liên tục và có sẵn nhiều ràng buộc. Nhưng các tính chất vật liệu phải được mô hình hóa trong một thiết lập liên tục. Điều này được thực hiện thông qua nội suy. Một trong những phương pháp nội suy được thực hiện nhiều nhất là phương pháp SIMP (Vật liệu đẳng hướng rắn với sự phạt[3]).[4] Nội suy này về cơ bản là một định luật dạng lũy thừa . Nó nội suy mô đun của vật liệu Young thành trường chọn vô hướng. Giá trị của tham số trừng phạt p thường được lấy giữa . Điều này đã xác nhận cấu trúc vi mô của vật liệu.[5] Trong phương pháp SIMP, giới hạn dưới của mô đun Young được thêm vào, , để đảm bảo các dẫn xuất của hàm mục tiêu khác 0 khi mật độ trở về 0. Hệ số phạt càng cao, càng nhiều SIMP xử lý thuật toán trong việc sử dụng mật độ không nhị phân. Thật không may, các tham số trừng phạt cũng xuất ra tính không lồi[6]).
Dẫn xuất hình dạng
[sửa | sửa mã nguồn]Các dẫn xuất topo
[sửa | sửa mã nguồn]Mức quy định
[sửa | sửa mã nguồn]Trường pha
[sửa | sửa mã nguồn]Tối ưu hóa cấu trúc tiến hóa
[sửa | sửa mã nguồn]Phần mềm thương mại
[sửa | sửa mã nguồn]Có một số phần mềm tối ưu hóa thương mại topo trên thị trường. Hầu hết trong số họ sử dụng tối ưu hóa Cấu trúc liên kết (Topology) như là một gợi ý thiết kế tối ưu sẽ như thế nào, và xây dựng lại hình học bằng tay là bắt buộc. Có một vài giải pháp tạo ra các thiết kế tối ưu sẵn sàng cho sản xuất đắp dần.
ParaMatters Inc., là công ty có trụ sở tại California, có thể tạo ra các cấu trúc hiệu suất rất cao bằng cách sử dụng tối ưu hóa topo với các bề mặt nhẵn và sẵn sàng cho sản xuất mà không cần phải tái tạo lại hình học. ParaMatters hỗ trợ tối ưu hóa Cấu trúc liên kết (Topology) xem xét các ràng buộc ứng suất, biến dạng, độ cứng và độ dao động.
Ví dụ
[sửa | sửa mã nguồn]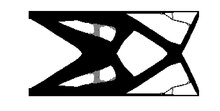


Tuân thủ cấu trúc
[sửa | sửa mã nguồn]Cấu trúc cứng là cấu trúc có khả năng dịch chuyển ít nhất có thể khi được đặt một số điều kiện biên nhất định. Một phép đo sự dịch chuyển toàn cục là năng lượng biến dạng (còn được gọi là sự tuân thủ) của cấu trúc theo các điều kiện biên được quy định. Ứng suất càng thấp thì độ cứng của cấu trúc càng cao. Vì vậy, tuyên bố vấn đề liên quan đến chức năng khách quan của năng lượng biến dạng cần phải được giảm thiểu.
Trên một mức độ rộng, người ta có thể hình dung rằng nhiều vật liệu, ít hơn sẽ là độ lệch vì có nhiều vật liệu hơn để chống lại tải trọng. Vì vậy, tối ưu hóa đòi hỏi một ràng buộc đối lập, hạn chế về khối lượng. Đây là thực tế là một yếu tố chi phí, vì chúng tôi sẽ không muốn chi nhiều tiền vào tài liệu. Để có được tổng số vật liệu được sử dụng, việc tích hợp trường chọn trên khối lượng có thể được thực hiện.
Cuối cùng, phương trình vi phân điều chỉnh độ đàn hồi được đưa vào để có được báo cáo vấn đề cuối cùng.
với:
Tuy nhiên, việc triển khai đơn giản trong Khung phần tử hữu hạn của vấn đề như vậy vẫn không khả thi do các vấn đề như:
- Sự phụ thuộc vào việc chia lưới - Phụ thuộc vào lưới có nghĩa là thiết kế thu được trên một lưới không phải là thiết kế sẽ thu được trên một lưới khác. Các tính năng của thiết kế trở nên phức tạp hơn khi lưới được làm mịn.
- Sự bất ổn định số — Việc lựa chọn khu vực dưới dạng một bàn cờ.
Một số kỹ thuật như lọc dựa trên xử lý hình ảnh hiện đang được sử dụng để giảm bớt một số vấn đề này.
Dạng 3F3D theo lực In 3D
[sửa | sửa mã nguồn]Sự gia tăng hiện tại của công nghệ Máy in 3D đã cho phép các nhà thiết kế và kỹ sư tận dụng các kỹ thuật tối ưu hóa cấu trúc liên kết khi thiết kế các sản phẩm mới.
Tối ưu hóa Cấu trúc liên kết (Topology) kết hợp với in 3D cho phép trọng lượng nhẹ đáng kể, cải thiện hiệu suất cấu trúc và rút ngắn chu trình thiết kế-sản xuất. [3] Lưu trữ 2018-03-11 tại Wayback Machine
Các vấn đề đa tạp
[sửa | sửa mã nguồn]Tham khảo
[sửa | sửa mã nguồn]- ^ Sigmund, O., Maute, K., Topology optimization approaches A comparative review. Structural and Multidisciplinary Optimization, 2013, p. 1031-1055
- ^ Beckers, M. Topology optimization using a duel method with discrete variables. Structural Optimization, p. 14-24
- ^ Bendsøe, MP. Optimal shape design as a material distribution problem.. Structural Optimization, 1989, p. 193-202
- ^ [1], a monograph of the subject.
- ^ [2], A reference that proved the validity of the interpolation scheme.
- ^ van Dijk, NP. Langelaar, M. van Keulen, F. Critical study of design parameterization in topology optimization; The influence of design parameterization on local minima.. 2nd International Conference on Engineering Optimization, 2010
- An efficient 3D topology optimization code written in Matlab K. Liu and A. Tovar; Int Journal of Structural and Multidisciplinary Optimization, doi:10.1007/s00158-014-1107-x, available from http://top3dapp.com
- Investigation into Structural Topology Optimization Problem Formulations, William Renold, lulu.com, 2007.
- Recent Developments in the Commercial Implementation of Topology Optimization[liên kết hỏng]; Uwe Schramm, Ming Zhou; IUTAM Symposium on Topological Design Optimization of Structures, Machines and Materials: Status and Perspectives, 239–248; 2006 Springer.
- Industrial Implementation and Applications of Topology Optimization and Future Needs Lưu trữ 2013-02-03 tại Archive.today; Claus B.W. Pedersen; Peter Allinger; IUTAM Symposium on Topological Design Optimization of Structures, Machines and Materials, 229-238; 2006 Springer.
- A 99 line topology optimization code written in Matlab[liên kết hỏng] Ole Sigmund; Int Journal of Structural and Multidisciplinary Optimization, Volume 21, 120-127, 2001 Springer
- Topology optimization of 2D continua for minimum compliance using parallel computing[liên kết hỏng] Arash Mahdavi; Balaji Raghavan; Mary Frecker; Int Journal of Structural and Multidisciplinary Optimization, Volume 32, 121-132, 2006 Springer
- Modern Structural Optimization Concepts Applied to Topology Optimization Lưu trữ 2018-01-19 tại Wayback Machine Juan Pablo Leiva; Brian C. Watson and Iku Kosaka; 40th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Material Conference. St. Louis, MO, pp. 1589–1596, 1999
- ToPy, an open source topology optimization program written in Python.
Liên kết ngoài
[sửa | sửa mã nguồn]- [4] - page containing information on the SIMP optimization method.
- Topology optimization animations
- Cloud-Based Topology Optimization - CogniCAD by ParaMatters Lưu trữ 2018-07-11 tại Wayback Machine








![{\displaystyle \scriptstyle [1,\,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6b426658716615e9685915e67165f541ca73885)


![{\displaystyle \scriptstyle \rho \,\in \,[0,\,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77d91d86c0e856662098acc3e592f71ab5cdeae4)


