Tích phân đường

Một phần của loạt bài về
Vi tích phân
Định lý cơ bản Quy tắc tích phân Leibniz Giới hạn của hàm số Tính liên tục Định lý giá trị trung bình Định lý Rolle
Vi phân Định nghĩa Đạo hàm (Tổng quát) Vi phân vô cùng bé hàm số toàn phần Khái niệm Ký hiệu vi phân Đạo hàm bậc hai Vi phân ẩn Định lý Taylor Quy tắc và đẳng thức Cộng Nhân Dây chuyền Lũy thừa Chia Quy tắc l'Hôpital Hàm ngược Leibniz tổng quát Công thức Faà di Bruno
Tích phân Danh sách tích phân Biến đổi tích phân Định nghĩa Nguyên hàm Tích phân (suy rộng) Tích phân Riemann Tích phân Lebesgue Tích phân theo chu tuyến Tích phân của hàm ngược Kỹ thuật Từng phần Đĩa Vỏ Thế (lượng giác, Weierstrass, Euler) Công thức Euler Đổi trật tự Công thức truy hồi Lấy đạo hàm dưới dấu tích phân
Chuỗi Hình học (số học-hình học) Điều hòa Đan dấu Lũy thừa Nhị thức Taylor Tiêu chuẩn hội tụ Số hạng d'Alembert Cauchy Tích phân So sánh So sánh giới hạn Chuỗi đan dấu Cô đọng Cauchy Dirichlet Abel
Vectơ Gradien Div Rot Laplace Đạo hàm có hướng Đẳng thức Định lý Gauss Gradient Green Kelvin–Stokes Stokes
Nhiều biến Chủ đề Ma trận Tenxơ Đạo hàm ngoài Hình học Định nghĩa Đạo hàm riêng Tích phân bội Tích phân đường Tích phân mặt Tích phân thể tích Ma trận Jacobi Ma trận Hesse
Chuyên ngành Malliavin Ngẫu nhiên Phép tính biến phân
Thuật ngữ Thuật ngữ giải tích

Trong toán học, tích phân đường là một phép tính tích phân khi hàm số được tích phân theo một đường.

Giải tích vectơ

Tích phân đường của trường vô hướng.

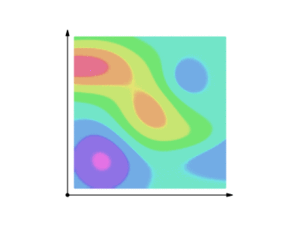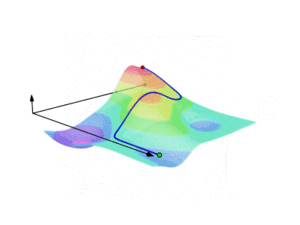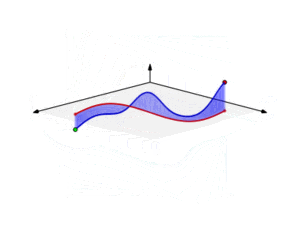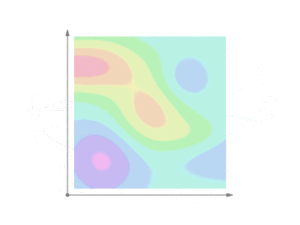
Một tích phân đường trong giải tích vecto có thể được xem như là một cách đo tổng ảnh hưởng của một trường cho trước dọc theo một đường cong cho trước. Cụ thể hơn, tích phân đường của một trường vô hướng có thể được diễn tả như là diện tích bên dưới trường đó được tạo ra bởi một đường cong nào đó. Điều này có thể tưởng tượng bằng cách xem mặt cong tạo ra bởi z = f(x,y) và một đường cong C trên mặt phẳng x-y. Tích phân đường của f sẽ là diện tích của bức "màn" tạo ra khi một điểm chuyển động ngay bên trên mặt của C tạo ra.

Định nghĩa

Với một trường vô hướng f: U ⊆ Rⁿ → R, một tích phân đường dọc theo một đường trơn gián đoạn C ⊂ U được định nghĩa như là

$\oint _{C}f\,ds=\int _{a}^{b}f(\mathbf {r} (t))|\mathbf {r} '(t)|\,dt.$

trong đó r: [a, b] → C là một tham số hóa của đường cong C sao cho r(a) và r(b) là hai điểm cuối của C.

Hàm số f được gọi là hạng tử tích phân, đường cong C là tập nguồn của tích phân, và ký hiệu ds có thể được diễn giải như là một đơn vị độ dài đường cong cơ bản. Tích phân đường của trường vô hướng theo một đường cong C không phụ thuộc vào cách tham số hóa r của C.

Tích phân đường của một trường vectơ

Với một trường vectơ F: U ⊆ Rⁿ → Rⁿ, tích phân đường dọc theo một đường cong trơn gián đoạn C ⊂ U, theo hướng của r, được định nghĩa bởi

$\oint _{C}\mathbf {F} (\mathbf {r} )\cdot \,d\mathbf {r} =\int _{a}^{b}\mathbf {F} (\mathbf {r} (t))\cdot \mathbf {r} '(t)\,dt.$

trong đó · là tích vô hướng và r: [a, b] → C là một tham số hóa song ánh của đường cong C sao cho r(a) và r(b) là hai điểm cuối của C.

Tích phân đường của một trường vô hướng do vậy chỉ là tích phân của một trường vectơ mà trong đó các vectơ luôn tiếp tuyến với đường cong đó.

Tích phân đường của trường vec tơ không phụ thuộc và tham số hóa r trong giá trị tuyệt đối, nhưng phụ thuộc vào định hướng của đường cong. Sự đảo ngược định hướng của đường cong sẽ làm thay đổi dấu của tích phân đường.