Luật Amdahl
Luật Amdahl, còn có tên Đối số Amdahl,[1] mang tên của kiến trúc sư máy tính Gene Amdahl. Nó được dùng để tìm ra sự cải thiện tối đa (theo mong đợi) của một hệ thống tổng thể khi chỉ cải thiện một phần của hệ thống. Nó còn được sử dụng trong tính toán song song để dự đoán sự tăng tốc trên lý thuyết khi sử dụng nhiều bộ xử lý (đa xử lý).
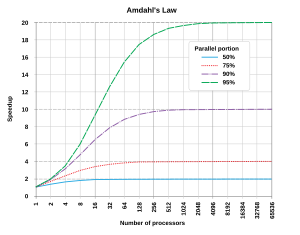
Sự tăng tốc của một chương trình đa xử lý trong tính toán song song bị giới hạn bởi thời gian cần thiết để thực hiện phần tính toán tuần tự của chương trình. Ví dụ nếu một bộ xử lý cần 20 giờ để thực hiện chương trình, và một phần của chương trình, tương ứng với 1 giờ thực hiện, không thể tính toán song song. 95% của chương trình (tương ứng với 19 giờ) có thể xử lý song song. Như vậy số bộ xử lý dùng trong tính toán song song lớn bao nhiêu chăng nữa, thời gian tối thiểu để thực hiện chương trình không thể nhỏ hơn 1 giờ. Như vậy sự tăng tốc chỉ là 20 lần, như biểu đồ bên phải.
Định nghĩa
[sửa | sửa mã nguồn]Luật Amdahl có thể được viết dưới dạng công thức sau đây:[2]
trong đó
- Slatency là sự tăng tốc về mặt lý thuyết của toàn bộ chương trình;
- s là sự tăng tốc của một phần chương trình nhờ vào sự cải thiện tài nguyên hệ thống;
- p là tỉ lệ của thời gian thực thi ban đầu.
Ngoài ra,
cho thấy rằng tốc độ về mặt lý thuyết của toàn bộ chương trình được tăng lên khi tài nguyên hệ thống được cải thiện, và bất kể cải thiện đến mức nào, sự tăng tốc lý thuyết luôn bị giới hạn bởi phần công việc không thể hưởng lợi từ sự cải thiện.
Luật Amdahl chỉ áp dụng trong những trường hợp kích thước bài toán là không đổi. Trong thực tế, tài nguyên máy tính lớn hơn thường được sử dụng cho các bài toán lớn hơn (các tập dữ liệu lớn hơn), và thời gian dành cho phần có thể tính toán song song thường tăng nhanh hơn đáng kể so với phần tính toán tuần tự. Trong trường hợp này, định luật Gustafson đưa ra một đánh giá ít bi quan hơn và thực tế hơn về hiệu suất tính toán song song.[3]
Miêu tả
[sửa | sửa mã nguồn]Luật Amdahl là một mô hình của mối quan hệ giữa sự tăng tốc mong đợi của việc triển khai song song của một thuật toán với phần tuần tự của thuật toán, với giả thiết rằng kích thước của bài toán không đổi khi tính toán song song. Ví dụ với kích thước bài toán cho trước phần thực hiện song song của thuật toán là 12%, có thể thực thi với tốc độ tuỳ ý, trong khi 88% còn lại không thể thực hiện song song, luật Amdahl cho biết rằng tốc độ tối đa của việc tính toán song song với thuật toán này chỉ nhanh hơn 1/(1 - 0,12) = 1,136 lần so với khi không có tính toán song song.
Chi tiết hơn, luật liên quan tới vấn đề tăng tốc có thể đạt được khi việc cải thiện một sự tính toán có thành phần cải thiện được là P và tăng tốc được S. Ví dụ nếu có thể cải thiện 30% sự tính toán thì P là 0,3; sự cải thiện này làm phần bị tác động tăng tốc gấp đôi thì S là 2. Luật Amdahl chỉ ra rằng tổng giá trị tăng tốc với sự cải thiện sẽ là
- .
Để thấy rõ hơn công thức này, giả sử rằng thời gian chạy của tính toán ban đầu là 1 đơn vị thời gian. Thời gian chạy của tính toán cải thiện là tổng thời gian của phần không cải thiện được (bằng 1 − P) với phần thời gian đã cải thiện. Thời gian của phần cải thiện bằng thời gian trước chia cho tốc độ cải thiện được, bằng P/S. Như vậy tốc độ cải thiện sau cùng được tính bằng thời gian chạy cũ chia cho thời gian mới, ra được công thức trên.
Xét thêm một ví dụ khác: có một công việc có thể chia thành 4 phần với tỉ lệ phần trăm như sau: P1 = 11%, P2 = 18%, P3 = 23%, P4 = 48% (tổng là 100%). P1 không thể tăng tốc tính toán, do vậy S1 = 1 hay 100%, P2 có thể tăng tốc lên 5 lần, do đó S2 = 500%, P3 có thể tăng tốc lên 20 lần, vậy S3 = 2000% và P4 tăng tốc được 1,6 lần, có S4 = 160%. Sử dụng công thức P1/S1 + P2/S2 + P3/S3 + P4/S4, ta thu được thời gian chạy là
- 0,11/1 + 0,18/5 + 0,23/20 + 0,48/1.6 = 0.4575
hay giảm được hơn một nửa thời gian ban đầu nếu giả sử ban đầu là 1. Vậy cả công việc có thể tăng tốc lên 1/0,4575 = 2,186 lần (hay hơn 2 lần) nhờ sử dụng công thức tính toán (P1/S1 + P2/S2 + P3/S3 + P4/S4)−1. Chú ý rằng việc tăng tốc những phần việc lên 20 lần và 5 lần không ảnh hưởng nhiều đến toàn bộ công việc vì gần một nửa phần việc chỉ có thể tăng tốc 1,6 lần.
Chú thích
[sửa | sửa mã nguồn]- ^ Rodgers 85, p.226
- ^ Bryant, Randal E.; David, O'Hallaron (2016), Computer Systems: A Programmer's Perspective (ấn bản thứ 3), Pearson Education, tr. 58, ISBN 978-1-488-67207-1
- ^ McCool, Michael; Reinders, James; Robison, Arch (2013). Structured Parallel Programming: Patterns for Efficient Computation. Elsevier. tr. 61. ISBN 978-0-12-415993-8.
Tham khảo
[sửa | sửa mã nguồn]- Gene Amdahl, "[1] Validity of the Single Processor Approach to Achieving Large-Scale Computing Capabilities", AFIPS Conference Proceedings, (30), pp. 483–485, 1967. Note: Gene Amdahl has approved the use of his complete text in the Usenet comp.sys.super news group FAQ which goes out on the 20th of each month.
- Rodgers, David P. (1985) Improvements in multiprocessor system design ACM SIGARCH Computer Architecture News archive Volume 13, Issue 3 (tháng 6 năm 1985) table of contents Special Issue: Proceedings of the 12th annual International Symposium on Computer Architecture (ISCA '85) Pages: 225 - 231 Year of Publication: 1985 ISSN:0163-5964. Also published in International Symposium on Computer Architecture, Proceedings of the 12th annual international symposium on Computer architecture, 1985, Boston, Massachusetts, United States
Liên kết ngoài
[sửa | sửa mã nguồn]- Gene Amdahl. Oral history interview. Lưu trữ 2002-06-12 tại Wayback Machine Charles Babbage Institute, University of Minnesota, Minneapolis.
- Reevaluating Amdahl's Law Lưu trữ 2012-06-23 tại Wayback Machine
- Reevaluating Amdahl's Law and Gustafson's Law Lưu trữ 2010-12-28 tại Wayback Machine
- A simple interactive Amdahl's Law calculator
- "Amdahl's Law" by Joel F. Klein, The Wolfram Demonstrations Project, 2007.
- Amdahl's Law in the Multicore Era
- Blog Post: "What the $#@! is Parallelism, Anyhow?" Lưu trữ 2008-09-09 tại Wayback Machine


![{\displaystyle {\begin{cases}S_{\text{latency}}(s)\leq {\dfrac {1}{1-p}}\\[8pt]\lim \limits _{s\to \infty }S_{\text{latency}}(s)={\dfrac {1}{1-p}}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5704c5d1949dcb3e9f130c974acb3a742e2cf4be)
