Định lý Đào về sáu tâm đường tròn

Đối với các định nghĩa khác, xem Định lý Đào (hình học).

Định lý Đào về sáu tâm đường tròn

Định lý Đào về sáu tâm đường tròn còn có tên đầy đủ là định lý Đào về sáu tâm đường tròn kết hợp với một lục giác nội tiếp một định lý trong lĩnh vưc hình học phẳng nói về mối quan hệ đồng quy của ba đường thẳng, mỗi đường thẳng đi qua tâm của hai đường tròn ngoại tiếp tam giác trong cấu trúc hình học liên quan tới một lục giác nội tiếp. Nội dung định lý như sau:

Cho một lục giác nội tiếp, khi đó đường thẳng nối tâm của các đường tròn ngoại tiếp của các tam giác đối diện mà các tam giác này tạo bởi một cạnh của lục giác và giao điểm của đường thẳng kéo dài của hai cạnh liền kề của cạnh đó sẽ đồng quy.

Giới thiệu

Đào Thanh Oai đề xuất một vấn đề về hình học trên trang Cut-The-Knot với tiêu đề là Another seven circles theorem, tiếng Việt: Định lý khác về bảy đường tròn, vào năm 2013. Sau đó gần một năm (năm 2014), định lý được Nikolaos Dergiades, nhà nghiên cứu toán học người Hy Lạp và một học sinh tại Đài Loan là Telv Cohl công bố với hai chứng minh độc lập..

Theo lời giới thiệu khi công bố trên bài báo của Nikolaos Dergiades tại tạp chí Forum Geometricorum của khoa toán đại học Florida Atlantic: "Định lý Đào về sáu tâm đường tròn được cho là một định lý đẹp Định lý Đào về sáu tâm đường tròn được cho là mới trong một bài nhận xét đăng trong cơ sở dữ liệu toán học Zentralblatt MATH.

Nikolao Dergiades tính toán bằng phương pháp tọa độ tỉ cự tính toán bằng phần mềm Mathematica kết quả cho điểm đồng quy dài hơn 72 trang A4.

Trong Bách khoa toàn thư về các tâm của tam giác một trường hợp đặc biệt của định lý Đào được thể hiện qua điểm $X_{3649}$. Trường hợp này được phát biểu như sau: Gọi $A'B'C'$ là tam giác bàn đạp ứng với tâm nội tiếp của tam giác $ABC$ khi đó tam giác tạo bởi tâm ba đường tròn ngoại tiếp các tam giác $AB'C'$, $BC'A'$, $CA'B'$ sẽ thấu xạ với tam giác $A'B'C'$ tại điểm $X_{3649}$. Điểm này chính là điểm Kosnita của tam giác $A'B'C'$.

Một số chứng minh

Mặc dù phương pháp tọa độ tỉ cự cho kết quả rất dài nhưng các chứng minh cho định lý này cũng khá ngắn gọn. Bài báo của Nikolaos Dergiades sử dụng phương pháp số phức để chứng minh định lý Đào, với tiêu đề tiếng Anh là Dao's theorem on six circumcenters associated with a cyclic hexagon (tạm dịch sang tiếng Việt là Định lý Đào về sáu tâm đường tròn kết hợp với một lục giác nội tiếp). Tác giả Telv Cohl chứng minh định lý Đào hoàn toàn thuần túy bằng hình học cổ điển.. Gregoire Nicollier đưa ra một chứng minh thông qua tính toán cho định lý này năm 2016.. Một số chứng minh khác đưa ra bởi hai người Việt Nam là Nguyễn Minh Hà và Nguyễn Tiến Dũng vào năm 2017, có thể xem tại đây .

Một phiên bản của định lý Đào đưa ra bởi Nguyễn Ngọc Giang nếu thay đường tròn bởi đường conic có thể xem tại đây .

Một số vấn đề liên quan

Một số vấn đề liên quan: Khi ba cặp đường chéo chính đồng quy thì sáu điểm là giao điểm thứ hai của các đường tròn liền kề nằm trên một đường tròn (Ngô Quang Dương)

Khi lục giác suy biến thành một tam giác, định lý Đào suy biến thành định lý Kosnita

Cho sáu đường thẳng $L_{1},L_{2},L_{3},L_{4},L_{5},L_{6}$, lấy module 6. Gọi $P_{ij}=L_{i}\cap L_{j}$, sao cho $P_{12},P_{23},P_{34},P_{45},P_{56},P_{61}$ nằm trên một đường tròn. Gọi $(O_{ijk})$ là đường tròn ngoại tiếp $(P_{ij},P_{jk},P_{ik})$ với tâm $O_{ijk}$. Gọi $P'_{ij}$ là giao điểm còn lại của $(O_{ijk})$ và $(O_{jkh})$. Khi đó ta có một số kết quả sau đây:

• Tâm đẳng phương của ba đường tròn $(O_{123})$, $(O_{345})$, $(O_{561})$ trùng với tâm đẳng phương của ba đường tròn $(O_{234})$, $(O_{456})$, $(O_{612})$
• Sáu đường tròn $(P_{12}P_{23}P_{24})$, $(P_{24}P_{34}P_{35})$, $(P_{35}P_{45}P_{46})$, $(P_{46}P_{56}P_{51})$, $(P_{51}P_{61}P_{62})$, $(P_{62}P_{12}P_{13})$ có chung tâm đẳng phương.
• Hai tam giác $O_{123}O_{345}O_{561}$ và $P_{24}P_{46}P_{62}$ là trực giao với nhau.
• Nếu ba cặp đường chéo chính $P_{12}P_{45},P_{34}P_{61},P_{56}P_{23}$ đồng quy thì sáu tâm đường tròn $O_{123}$, $O_{234}$, $O_{345}$, $O_{456}$, $O_{561}$, $O_{612}$ nằm trên một đường conic.
• Nếu ba cặp đường chéo chính $P_{12}P_{45},P_{34}P_{61},P_{56}P_{23}$ đồng quy. Khi đó sáu đường tròn $(O_{123})$, $(O_{234})$, $(O_{345})$, $(O_{456})$, $(O_{561})$, $(O_{612})$ có chung một tâm đẳng phương.
• Nếu ba cặp đường chéo chính$P_{12}P_{45},P_{34}P_{61},P_{56}P_{23}$ đồng quy. Khi đó $P'_{12}$, $P'_{23}$, $P'_{34}$, $P'_{45}$, $P'_{56}$, $P'_{61}$ nằm trên một đường tròn.

Trường hợp đặc biệt

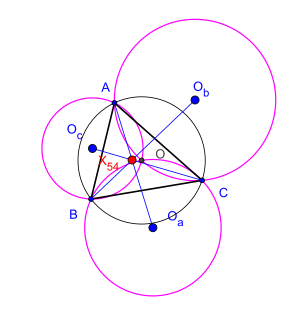
Trường hợp lục giác suy biến thành tam giác định lý Đào về sáu tâm đường tròn sẽ trực tiếp suy biến thành định lý Kosnita. Định lý Kosnita phát biểu như sau: Cho tam giác $ABC$ có $O$ là tâm đường tròn ngoại tiếp, $O_{a}$, $O_{b}$, $O_{c}$ là tâm các đường tròn ngoại tiếp tam giác $OBC$, $OCA$, $OAB$ thì $AO_{a}$, $BO_{b}$, $CO_{c}$ đồng quy.

Xem thêm

• Định lý Desargues
• Định lý Kosnita
• Định lý Đào (conic)
• Định lý tám đường tròn

Liên kết ngoài

• Hình vẽ động của Định lý Đào về sáu tâm đường tròn kết hợp với một lục giác nội tiếp, geogebratube.
• Các kết quả đã công bố trên tạp chí, Dao's blog
• Contact Triangle at MathWorld