Đáp ứng tần số
Trang hay phần này đang được viết mới, mở rộng hoặc đại tu. Bạn cũng có thể giúp xây dựng trang này. Nếu trang này không được sửa đổi gì trong vài ngày, bạn có thể gỡ bản mẫu này xuống. Nếu bạn là người đã đặt bản mẫu này, đang viết bài và không muốn bị mâu thuẫn sửa đổi với người khác, hãy treo bản mẫu {{đang sửa đổi}}.Sửa đổi cuối: Cheminiwawaky (thảo luận · đóng góp) vào 46 ngày trước. (làm mới) |
Đáp ứng tần số là phép đo định lượng của phổ đầu ra của một hệ thống hoặc thiết bị khi phản ứng với một kích thích, và được sử dụng để mô tả động lực học của hệ thống đó. Nó là một đo lường của biên độ và pha của đầu ra như là một hàm của tần số, so với đầu vào. Trong điều kiện đơn giản nhất, nếu một sóng sin được đưa vào một hệ thống ở một tần số cho trước, một hệ thống tuyến tính sẽ đáp ứng ở cùng tần số đó với một cường độ và một góc pha nhất định tương đối so với đầu vào. Cũng đối với một hệ thống tuyến tính, khi tăng gấp đôi biên độ của đầu vào thì cũng sẽ tăng gấp đôi biên độ của đầu ra.
Hai ứng dụng của phân tích đáp ứng tần số có liên quan với nhau nhưng có những mục đích khác nhau. Đối với một hệ thống khuếch đại âm thanh, mục tiêu có thể là mô phỏng lại các tín hiệu đầu vào mà không bị biến dạng. Điều này đòi hỏi một biên độ đều (phẳng) của đáp ứng theo giới hạn băng thông của hệ thống, với tín hiệu bị trì hoãn bởi chính xác cùng một lượng thời gian ở tất cả các tần số. Thời gian có thể tính bằng giây, hoặc vài tuần hoặc vài tháng tùy vào phương tiện dùng để ghi lại. Ngược lại, đối với một bộ máy thông tin phản hồi được sử dụng để điều khiển một hệ thống động lực, mục tiêu là để cải thiện đáp ứng cho hệ thống vòng kín so với các hệ thống không được bù. Phản hồi nhìn chung cần phải đáp ứng cho các động lực học của hệ thống trong một lượng rất nhỏ của chu kỳ dao động (thường ít hơn một chu kỳ đầy đủ), và với một góc pha xác định quan hệ với lệnh điều khiển đầu vào. Đối với thông tin phản hồi của khuếch đại đầy đủ, nhận góc pha sai có thể dẫn đến sự mất ổn định cho hệ thống ổn định vòng hở, hoặc không thể ổn định một hệ thống mà có vòng hở không ổn định. Các bộ lọc kỹ thuật số có thể được sử dụng cho cả hệ thống khuếch đại âm thanh và hệ thống điều khiển phản hồi, nhưng vì các mục tiêu khác nhau, nhìn chung các đặc tính pha của các bộ lọc sẽ khác nhiều so với hai ứng dụng này.
Dự đoán và vẽ biểu đồ
[sửa | sửa mã nguồn]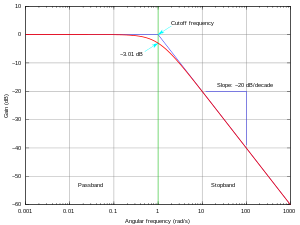
Dự đoán đáp ứng tần số cho một hệ thống vật lý nói chung bao gồm việc kích thích hệ thống đó với một tín hiệu đầu vào, đo lịch sử thời gian cả đầu vào và đầu ra, và so sánh cả hai thông qua một quá trình chẳng hạn như Biến đổi Fourier Nhanh (FFT). Một điều cần lưu ý khi phân tích là tần số bao gồm của tín hiệu đầu vào phải bao gồm các dải tần số quan tâm hoặc các kết quả sẽ không có hiệu lực đối với phần của dãy tần số không được tính đến.
Đáp ứng tần số của một hệ thống có thể được đo bằng cách dùng một tín hiệu kiểm tra, ví dụ:
- dùng một xung áp vào hệ thống và đo lường đáp ứng của nó (xem đáp ứng xung)
- Quét một âm thuần biên độ không đổi qua băng thông cần đo và đo mức độ và dịch chuyển pha đầu ra tương ứng với đầu vào
- Áp một tín hiệu với một phổ tần số rộng (ví dụ như nhiễu dãy chiều dài tối đa kỹ thuật số, hoặc bộ lọc analog nhiễu trắng tương đương, như nhiễu hồng), và tính toán đáp ứng xung bởi sự mở cuộn của tín hiệu đầu vào và tín hiệu đầu ra của hệ thống này.
Đáp ứng tần số được đặc trưng bởi biên độ của đáp ứng của hệ thống, thường được đo bằng decibels (dB) hoặc số thập phân, và pha, được đo bằng radian hoặc độ, so với tần số được đo bằng radian/giây hoặc Hertz (Hz).
Các phép đo đáp ứng này có thể được vẽ biểu đồ trong ba cách: bằng cách vẽ các đo lường biên độ và pha lên 2 biểu đồ hình chữ nhật như các hàm của tần số để có được một biểu đồ Bode; bằng cách vẽ biên độ và góc pha trên một biểu đồ đơn cực với tần số như là một tham số để có được một biểu đồ Nyquist; hoặc bằng cách vẽ biểu đồ biên độ và pha trên một biểu đồ hình chữ nhật duy nhất với tần số là một tham số để có được một biểu đồ Nichols.
Đối với các hệ thống âm thanh với gần như đồng thời gian trễ ở tất cả các tần số, biên đọ so với tần số của biểu đồ Bode có thể là tất cả những gì cần quan tâm. Để thiết kế các hệ thống điều khiển, bất kỳ loại biểu đồ nào trong ba loại [Bode, Nyquist, Nichols] cũng có thể được sử dụng để đưa ra kết luận về độ ổn định vòng kín và biên độ ổn định (độ lợi và biên độ pha) từ đáp ứng tần số vòng hở, miễn là bao gồm phân tích biểu đồ Bode pha so với tần số.
Đáp ứng tần số phi tuyến
[sửa | sửa mã nguồn]Nếu hệ thống được nghiên cứu là phi tuyến thì áp dụng các phân tích miền tần số tuyến tính thuần túy sẽ không thể hiện được tất cả các đặc tính phi tuyến. Để khắc phục những hạn chế của các hàm đáp ứng tần số nói chung, và các hàm đáp ứng tần số đầu ra phi tuyến đã được xác định cho phép người sử dụng để phân tích các hiệu ứng động học phi tuyến phức tạp.[1] Các phương pháp đáp ứng tần số phi tuyến thể hiện được cộng hưởng phức tạp, biến điệu tương hỗ, và các hiệu ứng biến đổi năng lượng mà không thể thấy được bằng cách sử dụng phương pháp phân tích hoàn toàn tuyến tính và đang trở nên ngày càng quan trọng trong một thế giới phi tuyến.
Ứng dụng
[sửa | sửa mã nguồn]Trong lĩnh vực điện tử kích thích này sẽ là một tín hiệu đầu vào.[2] Trong lĩnh vực khuếch đại âm thanh nó thường được nhắc đến trong kết nối với bộ khuếch đại điện tử, micro và loa. Đáp ứng tần số phổ radio có thể để nói tới các đo lường của cáp đồng trục, cáp xoắn đôi, thiết bị chuyển mạch video, thiết bị truyền thông không dây và các hệ thống ăng-ten. Các đo lường đáp ứng tần số hạ âm bao gồm động đất và điện não đồ (sóng não).
Tần số đáp ứng có các yêu cầu khác nhau tùy thuộc vào ứng dụng.[3] Trong khuếch đại âm thanh trung thực cao, một bộ khuếch đại đòi hỏi một phản ứng tần số ít nhất 20-20,000 Hz, với dung sai chính xác ± 0,1 dB trong các tần số trung tần khoảng 1000 Hz, tuy nhiên, trong viễn thông, đáp ứng tần số 400-4,000 Hz, với dung sai ± 1 dB là đủ để hiểu nội dung của cuộc hội thoại.[3]
Đồ thị đáp ứng tần số thường được sử dụng để chỉ ra tính chính xác của các thành phần điện tử hoặc hệ thống.[2] Khi một hệ thống hay thành phần tái tạo tất cả các tín hiệu đầu vào mong muốn mà không có bất kỳ cường điệu hoặc suy giảm nào của băng thông đặc biệt, hệ thống hoặc thành phần được gọi là "phẳng", hoặc có một đồ thị đáp ứng tần số phẳng.[2]
Khi một đáp ứng tần số được đo (ví dụ, như một đáp ứng xung), đã biết hệ thống đó là tuyến tính và thời gian bất biến, các đặc tính của nó có thể được xấp xỉ với độ chính xác tùy ý bởi một bộ lọc kỹ thuật số. Tương tự như vậy, nếu một hệ thống được chứng minh là có một đáp ứng tần số yếu, một bộ lọc analog hoặc kỹ thuật số có thể được áp dụng cho các tín hiệu đó trước khi chúng được tái tạo để bù đắp cho những thiếu hụt này.
Xem thêm
[sửa | sửa mã nguồn]- Đáp ứng xung
- Hàm truyền
- Biểu đồ Bode
- Băng thông (xử lý tín hiệu)
- Đo lường hệ thống âm thanh
- Đáp ứng quá độ & đáp ứng ổn định
- Độ nhạy phổ
Tham khảo
[sửa | sửa mã nguồn]- Ghi chú
- ^ Billings S.A. "Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains".
- ^ a b c Stark, 2002, p. 51.
- ^ a b Luther, 1999, p. 141.
- Tiểu sử
- Luther, Arch C.; Inglis, Andrew F. Video engineering, McGraw-Hill, 1999. ISBN 0-07-135017-9
- Stark, Scott Hunter. Live Sound Reinforcement, Vallejo, California, Artistpro.com, 1996–2002. ISBN 0-ngày 94 tháng 7 năm 8371
Liên kết ngoài
[sửa | sửa mã nguồn]- University of Michigan: Frequency Response Analysis and Design Tutorial Lưu trữ 2012-10-17 tại Wayback Machine
- Smith, Julius O. III: Introduction to Digital Filters with Audio Applications has a nice chapter on Frequency Response
